Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1 thiếu đề
Bài 2 Mình không vẽ được hình nên bạn thông cảm
Xét tam giác vuông ACO có \(CM\perp AO\)
=> \(OM.OA=OC^2=OD^2\)
=> \(\frac{OD}{OA}=\frac{OM}{OD}\)
=> tam giác MDO đồng dạng tam giác DAO
=> MDO=OAD
Mà MDO=DEO
=> OAD=DEO
=> tứ giác ADOE nội tiếp
Vậy tứ giác ADOE nội tiếp

b) Dễ thấy C là trực tâm của tam giác IAB nên C, I, H thẳng hàng.
Do tứ giác AICK là hình thang nội tiếp được đường tròn nên là hình thang cân.
Khi đó \(\widehat{IAK}=\widehat{CKA}\Rightarrow\widehat{IAB}=\widehat{NBA}\)
Suy ra tam giác NAB vuông cân tại N nên \(\widehat{NBA}=45^o\).
Ta có các tứ giác CMIN, AMIH nội tiếp được nên \(\widehat{NMH}=\widehat{NMI}+\widehat{HMI}=\widehat{ICN}+\widehat{IAB}=45^o+45^o=90^o\Rightarrow MN\perp MH\).

c) Đề phải là \(\dfrac{IC}{IH}+\dfrac{IA}{IN}+\dfrac{IB}{IM}\ge6\).
Đặt \(x=\dfrac{IH}{CH};y=\dfrac{IN}{AN};z=\dfrac{IM}{BM}\left(x,y,z< 1\right)\).
Ta có \(x+y+z=\dfrac{S_{IAB}}{S_{ABC}}+\dfrac{S_{IBC}}{S_{ABC}}+\dfrac{S_{ICA}}{S_{ABC}}=1\).
Lại có \(\dfrac{IH}{CH}=x\Rightarrow\dfrac{CH}{IH}=\dfrac{1}{x}\Rightarrow\dfrac{IC}{IH}=\dfrac{1}{x}-1\).
Tương tự \(\dfrac{IA}{IN}=\dfrac{1}{y}-1;\dfrac{IB}{IM}=\dfrac{1}{z}-1\).
Do đó \(\dfrac{IC}{IH}+\dfrac{IA}{IN}+\dfrac{IB}{IM}=\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}-3\ge_{Svacxo}\dfrac{9}{x+y+z}-3=\dfrac{9}{1}-3=6\).
Vậy ta có đpcm.

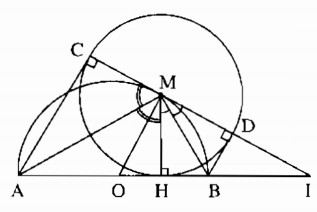
A B M H O C D I
a) Áp dụng tính chất hai tiếp tuyến giao nhau: ^HMC = 2.^AMH; ^HMD = 2.^BMH
Suy ra ^HMC + ^HMB = 2(^AMH + ^BMH) = 1800 => 3 điểm C,M,D thẳng hàng (đpcm).
Có C,M,D thẳng hàng, Do C,D thuộc (M;MH) nên CD là đường kính của (M;MH)
Khi đó MO là đường trung bình của hình thang vuông ACDB => MO // AC // BD
=> MO vuông góc CD => CD là tiếp tuyến của (O) (đpcm).
b) Dễ thấy AC + BD = AH + BH = 2R (R là bán kính của (O)) (không đổi).
c) Áp dụng hệ thức lượng trong tam giác vuông IMO có OH.OI = OM2 = R2 (không đổi).