Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

O A B M I
Gọi I là trung điêm OM
do đó ta có tính chất của trung tuyến ứng với cạnh huyền lầ
\(IO=IA=IM=\frac{1}{2}OM=\frac{1}{2}.2R=R\)
Xét tam giác IOA có \(IO=OA=AI=R\Rightarrow\)tam giác IOA đều nên IOA = 60 độ
chứng minh tương tự ta sẽ có góc IOB=60 độ
nên AOB=AOI+IOB=120 độ

a: Xét tứ giác OAMB có
góc OAM+góc OBM=180 độ
nên OAMB là tứ giác nội tiêp
b: Xét (O) có
MA,MB là tiếp tuyến
nên MA=MB
mà OA=OB
nên OM là trung trực của AB
=>OM vuông góc với AB

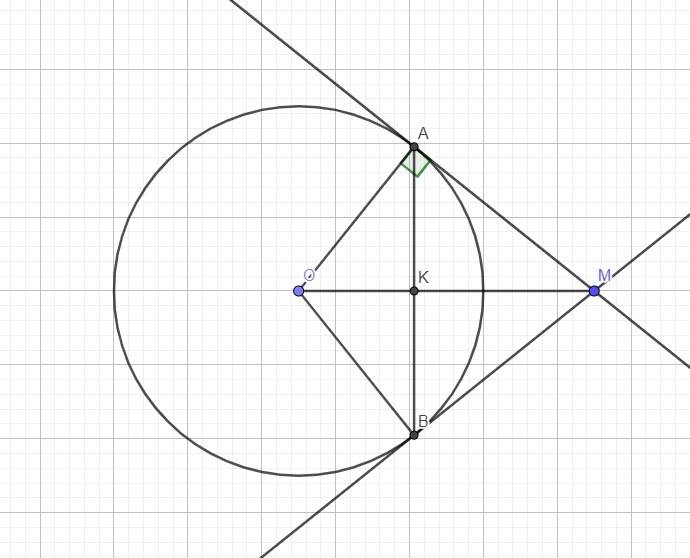
Bài 7:
a: Xét ΔOAM vuông tại A có
\(\cos\widehat{AOM}=\dfrac{OA}{OM}=\dfrac{1}{2}\)
nên \(\widehat{AOM}=60^0\)
b: Xét tứ giác OAMB có
\(\widehat{OAM}+\widehat{OBM}=180^0\)
Do đó: OAMB là tứ giác nội tiếp
Suy ra: \(\widehat{AOB}=180^0-36^0=144^0\)

Do MA là tiếp tuyến \(\Rightarrow OA\perp MA\) hay tam giác OAM vuông tại A
Áp dụng định lý Pitago:
\(MA=\sqrt{OM^2-OA^2}=\sqrt{\left(\dfrac{8R}{5}\right)^2-R^2}=\dfrac{R\sqrt{39}}{5}\)
Theo t/c hai tiếp tuyến cắt nhau ta có \(AM=BM\)
Mà \(OA=OB=R\Rightarrow OM\) là trung trực AB \(\Leftrightarrow\left\{{}\begin{matrix}OM\perp AB\\AK=BK\end{matrix}\right.\)
Áp dụng hệ thức lượng trong tam giác vuông OAM:
\(AK.OM=OA.AM\Rightarrow AK=\dfrac{OA.AM}{OM}=\dfrac{R\sqrt{39}}{8}\)
\(\Rightarrow AB=2AK=\dfrac{R\sqrt{39}}{4}\)
Áp dụng định lý Pitago trong tam giác vuông AOK:
\(OK=\sqrt{OA^2-AK^2}=\sqrt{R^2-\left(\dfrac{R\sqrt{39}}{8}\right)^2}=\dfrac{5R}{8}\)

a: góc OAM+góc OBM=90+90=180 độ
=>AOBM nội tiếp
b: góc BOM=1/2*góc AOB=góc BCA
a giải thích em làm sao 1/2 AOB = góc BCA được ạ

a: OH*OM=OA^2=R^2
b: ΔOCD cân tại O
mà OI là đường trung tuyến
nên OI vuông góc với CD
Xét tứ giác OIAM có
góc OIM=góc OAM=90 độ
nên OIAM là tứ giác nội tiếp
c: Xét ΔOHK vuông tại H và ΔOIM vuông tại I có
góc HOK chung
Do đo: ΔOHK đồng dạng với ΔOIM
=>OH/OI=OK/OM
=>OI*OK=OH*OM=R^2=OC^2
mà CI vuông góc với OK
nên ΔOCK vuông tại C
=>KC là tiếp tuyến của (O)

O' O B C K Y A
a) Ta thấy ngay AY chính là tiếp tuyến chung của hai đường tròn (O) và (O')
Theo tính chất hai tiếp tuyến cắt nhau, ta có YB = YA = YC
Vậy nên tam giác BAC vuông tại A hay \(\widehat{BAC}=90^o\)
b) Theo tính chất hai tiếp tuyến cắt nhau ta có \(\widehat{AYO}=\widehat{OYB};\widehat{AYO'}=\widehat{O'YC}\)
\(\Rightarrow\widehat{OYO'}=\widehat{OYA}+\widehat{AYO'}=90^o\)
Xét tam giác vuông OYO' có YK là trung tuyến ứng với cạnh huyền nên \(KY=\frac{OO'}{2}\)
c) Ta thấy ngay BOO'C là hình thang vuông có Y là trung điểm BC, K là trung điểm OO' nên KY là đường trung bình của hình thang.
Vậy thì KY // OB // O'C
Từ đó ta có ngay KY vuông góc BC.
Lại có \(KY=KO\)
Nên BC là tiếp tuyến của đường tròn tâm K, bán kính KO.