Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Dạng \(u_{n+1}=\dfrac{au_n+b}{cu_n+d}\) này có 1 cách làm chung:
Đặt \(v_n=u_n+k\) với k sao cho sau khi chuyển vế rút gọn thì tử số của \(\dfrac{au_n+b}{cu_n+d}\) triệt tiêu mất số hạng tự do b là được.
Ví dụ ở bài này, ta đặt ra nháp:
\(u_n=v_n+k\Rightarrow v_{n+1}+k=\dfrac{4\left(v_n+k\right)+2}{v_n+3+k}\)
\(\Rightarrow v_{n+1}=\dfrac{4v_n+4k+2}{v_n+k+3}-k=\dfrac{4v_n+4k+2-k\left(v_n+k+3\right)}{v_n+k+3}\)
\(=\dfrac{\left(4-k\right)v_n+2-k^2+k}{v_n+k+3}\)
Cần k sao cho \(-k^2+k+2=0\Rightarrow k=-1\) (lấy số nhỏ cho gọn). Vậy là xong. Thực tế ta làm như sau:
Đặt \(u_n=v_n-1\Rightarrow v_1=u_1+1=4\)
\(v_{n+1}-1=\dfrac{4\left(v_n-1\right)+2}{v_n+2}\Rightarrow v_{n+1}=\dfrac{4v_n-2}{v_n+2}+1=\dfrac{5v_n}{v_n+2}\)
(sau đó nghịch đảo 2 vế):
\(\Rightarrow\dfrac{1}{v_{n+1}}=\dfrac{v_n+2}{5v_n}=\dfrac{2}{5}.\dfrac{1}{v_n}+\dfrac{1}{5}\)
(Đây là gần như 1 dãy bình thường rồi)
(Tiếp tục đặt \(\dfrac{1}{v_n}=x_n+k\) sao cho triệt tiêu nốt số hạng \(\dfrac{1}{5}\) bên phải đi:
\(x_{n+1}+k=\dfrac{2}{5}\left(x_n+k\right)+\dfrac{1}{5}\Rightarrow x_{n+1}=\dfrac{2}{5}.x_n+\dfrac{2k}{5}+\dfrac{1}{5}-k\)
\(\Rightarrow\dfrac{2k}{5}+\dfrac{1}{5}-k=0\Rightarrow k=\dfrac{1}{3}\))
Đặt \(\dfrac{1}{v_n}=x_n+\dfrac{1}{3}\Rightarrow x_1=\dfrac{1}{v_1}-\dfrac{1}{3}=\dfrac{1}{4}-\dfrac{1}{3}=-\dfrac{1}{12}\)
\(\Rightarrow x_{n+1}+\dfrac{1}{3}=\dfrac{2}{5}\left(x_n+\dfrac{1}{3}\right)+\dfrac{1}{5}\Leftrightarrow x_{n+1}=\dfrac{2}{5}x_n\)
Đây là công thức cấp số nhân dạng , do đó ta có: \(x_n=-\dfrac{1}{12}.\left(\dfrac{2}{5}\right)^{n-1}\)
\(\Rightarrow\dfrac{1}{v_n}=x_n+\dfrac{1}{3}=-\dfrac{1}{12}.\left(\dfrac{2}{5}\right)^{n-1}+\dfrac{1}{3}=-\dfrac{2^{n-1}}{12.5^{n-1}}+\dfrac{4.5^{n-1}}{12}=\dfrac{4.5^{n-1}-2^{n-1}}{12.5^{n-1}}\)
\(\Rightarrow v_n=\dfrac{12.5^{n-1}}{4.5^{n-1}-2^{n-1}}\)
\(\Rightarrow u_n=v_n-1=\dfrac{12.5^{n-1}}{4.5^{n-1}-2^{n-1}}-1\)
\(lim\left(u_n+4\right)=lim\left(\dfrac{12.5^{n-1}}{4.5^{n-1}-2^{n-1}}+3\right)=\dfrac{12}{4}+3=6\)
Đây là cách làm cơ bản, còn trên thực tế, khi trắc nghiệm chỉ cần đơn giản như sau:
Giả sử \(lim\left(u_n\right)=a\), hiển nhiên dãy đã cho dương nên a dương
Lấy giới hạn 2 vế giả thiết:
\(lim\left(u_{n+1}\right)=lim\left(\dfrac{4u_n+2}{u_n+3}\right)\Rightarrow a=\dfrac{4a+2}{a+3}\)
\(\Rightarrow a^2+3a=4a+2\)
\(\Rightarrow a^2-a-2=0\Rightarrow\left[{}\begin{matrix}a=-1\\a=2\end{matrix}\right.\) \(\Rightarrow a=2\)
\(\Rightarrow lim\left(u_n+4\right)=2+4=6\)
Nhanh hơn khoảng 1 tỉ lần :D

Lời giải:
Bằng quy nạp ta dễ chứng minh được $u_n< 1$
$u_{n+1}-u_n=\frac{1}{2-u_n}-u_n=\frac{(u_n-1)^2}{2-u_n}>0$ với mọi $u_n< 1$
$\Rightarrow u_{n+1}>u_n$. Vậy $(u_n)$ là dãy tăng và bị chặn trên.
Gọi $\lim u_n=a$ thì $a=\frac{1}{2-a}\Rightarrow 2a-a^2=1$
$\Leftrightarrow (a-1)^2=0\Leftrightarrow a=1$
Đáp án B

Số xấu thế nhỉ?
\(u_n=v_n+\dfrac{\sqrt{5}-3}{2}\)
\(\Rightarrow v_{n+1}+\dfrac{\sqrt{5}-3}{2}=-\dfrac{1}{3+v_n+\dfrac{\sqrt{5}-3}{2}}\)
\(\Rightarrow\left\{{}\begin{matrix}v_1=u_1-\dfrac{\sqrt{5}-3}{2}=\dfrac{5-\sqrt{5}}{2}\\v_{n+1}=\dfrac{\dfrac{3-\sqrt{5}}{2}v_n}{\dfrac{3+\sqrt{5}}{2}+v_n}\end{matrix}\right.\)
\(v_n=\dfrac{1}{y_n}\Rightarrow\dfrac{1}{y_{n+1}}=\dfrac{\dfrac{3-\sqrt{5}}{2}.\dfrac{1}{y_n}}{\dfrac{3+\sqrt{5}}{2}+\dfrac{1}{y_n}}\)
\(\Rightarrow\dfrac{1}{y_{n+1}}=\dfrac{3-\sqrt{5}}{2y_n\left(\dfrac{3+\sqrt{5}}{2}+\dfrac{1}{y_n}\right)}=\dfrac{3-\sqrt{5}}{\left(3+\sqrt{5}\right)y_n+2}\)
\(\Leftrightarrow y_{n+1}=\dfrac{\left(3+\sqrt{5}\right)y_n}{3-\sqrt{5}}+\dfrac{2}{3-\sqrt{5}}\)
\(\Rightarrow\left\{{}\begin{matrix}y_1=\dfrac{1}{v_1}=\dfrac{2}{5-\sqrt{5}}\\y_{n+1}=\dfrac{3+\sqrt{5}}{3-\sqrt{5}}y_n+\dfrac{2}{3-\sqrt{5}}\end{matrix}\right.\)
\(z_n=y_n+\dfrac{\sqrt{5}}{5}\Rightarrow\left\{{}\begin{matrix}z_1=y_1+\dfrac{\sqrt{5}}{5}=\dfrac{5+3\sqrt{5}}{10}\\z_{n+1}=\dfrac{3+\sqrt{5}}{3-\sqrt{5}}z_n\end{matrix}\right.\)
\(\Rightarrow z_n:csn-co:\left\{{}\begin{matrix}z_1=\dfrac{5+3\sqrt{5}}{10}\\q=\dfrac{3+\sqrt{5}}{3-\sqrt{5}}\end{matrix}\right.\)
\(\Rightarrow z_{n+1}=\dfrac{5+3\sqrt{5}}{10}.\left(\dfrac{3+\sqrt{5}}{3-\sqrt{5}}\right)^n\)
\(\Rightarrow y_{n+1}=z_{n+1}-\dfrac{\sqrt{5}}{5}=\dfrac{5+3\sqrt{5}}{10}\left(\dfrac{3+\sqrt{5}}{3-\sqrt{5}}\right)^n-\dfrac{\sqrt{5}}{5}\)
\(v_{n+1}=\dfrac{1}{y_{n+1}}=\dfrac{1}{\dfrac{5+3\sqrt{5}}{10}\left(\dfrac{3+\sqrt{5}}{3-\sqrt{5}}\right)^n-\dfrac{\sqrt{5}}{5}}\)
\(u_{n+1}=v_{n+1}+\dfrac{\sqrt{5}-3}{2}=\dfrac{1}{\dfrac{5+3\sqrt{5}}{10}\left(\dfrac{3+\sqrt{5}}{3-\sqrt{5}}\right)^n-\dfrac{\sqrt{5}}{5}}+\dfrac{\sqrt{5}-3}{2}\)
Xét:
\(u_{n+2}-u_{n+1}=\dfrac{1}{\dfrac{5+3\sqrt{5}}{10}.\left(\dfrac{3+\sqrt{5}}{3-\sqrt{5}}\right)^n.\left(\dfrac{3+\sqrt{5}}{3-\sqrt{5}}\right)-\dfrac{\sqrt{5}}{5}}+\dfrac{\sqrt{5}-2}{2}-\dfrac{1}{\dfrac{5+3\sqrt{5}}{10}\left(\dfrac{3+\sqrt{5}}{3-\sqrt{5}}\right)^n-\dfrac{\sqrt{5}}{5}}-\dfrac{\sqrt{5}-2}{2}\)
\(=\dfrac{1}{\dfrac{5+3\sqrt{5}}{10}\left(\dfrac{3+\sqrt{5}}{3-\sqrt{5}}\right)^n.\dfrac{3+\sqrt{5}}{3-\sqrt{5}}-\dfrac{\sqrt{5}}{5}}-\dfrac{1}{\dfrac{5+3\sqrt{5}}{10}\left(\dfrac{3+\sqrt{5}}{3-\sqrt{5}}\right)^n-\dfrac{\sqrt{5}}{5}}\)
\(=\dfrac{\dfrac{5+3\sqrt{5}}{10}\left(\dfrac{3+\sqrt{5}}{3-\sqrt{5}}\right)^n-\dfrac{5+3\sqrt{5}}{10}\left(\dfrac{3+\sqrt{5}}{3-\sqrt{5}}\right)^n.\left(\dfrac{3+\sqrt{5}}{3-\sqrt{5}}\right)}{.....}\)
\(=\dfrac{\dfrac{5+3\sqrt{5}}{10}\left(\dfrac{3+\sqrt{5}}{3-\sqrt{5}}\right)^n\left(1-\dfrac{3+\sqrt{5}}{3-\sqrt{5}}\right)}{....}=\dfrac{\dfrac{5+3\sqrt{5}}{10}\left(\dfrac{3+\sqrt{5}}{3-\sqrt{5}}\right)^n.\left(-\dfrac{5+3\sqrt{5}}{2}\right)}{...}< 0\)
\(\Rightarrow\) dãy giảm
\(\Rightarrow u_1>u_2>....>u_n\)
\(\Rightarrow\lim\limits u_n=1\)
Bn tham khảo đây nhé: https://diendantoanhoc.org/topic/140204-t%C3%A0i-li%E1%BB%87u-d%C3%A3y-s%E1%BB%91/

\(u_{n+1}=\dfrac{u_n}{u_n+1}\Rightarrow\dfrac{1}{u_{n+1}}=\dfrac{1}{u_n}+1\)
Đặt \(\dfrac{1}{u_n}=v_n\Rightarrow\left\{{}\begin{matrix}v_1=\dfrac{1}{u_1}=1\\v_{n+1}=v_n+1\end{matrix}\right.\)
\(\Rightarrow v_n\) là CSC với công sai \(d=1\Rightarrow v_n=v_1+\left(n-1\right).1=n\)
\(\Rightarrow u_n=\dfrac{1}{n}\)
\(\Rightarrow u_n+1=\dfrac{n+1}{n}\)
\(\lim\dfrac{2014\left(\dfrac{2}{1}\right)\left(\dfrac{3}{2}\right)\left(\dfrac{4}{3}\right)...\left(\dfrac{n+1}{n}\right)}{2015n}=\lim\dfrac{2014\left(n+1\right)}{2015n}=\dfrac{2014}{2015}\)
https://hoc24.vn/cau-hoi/giai-phuong-trinhleft3-4sin2xrightleft3-4sin23xright1-2cos10x.4916575957961
Giúp mik bài này với ạ
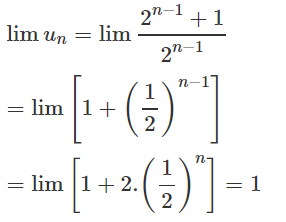

Là 6