Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét (O) có
ΔBDC nội tiếp đường tròn
BC là đường kính
Do đó: ΔBDC vuông tại D
Xét (O) có
ΔBEC nội tiếp đường tròn
BC là đường kính
Do đó: ΔBEC vuông tại E

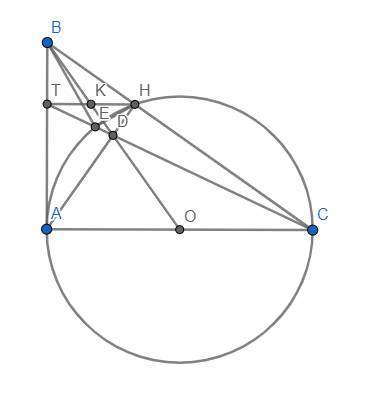
Gọi T là giao điểm của CD và AB. Khi đó xét tứ giác ACHT, ta có:
O (trung điểm AC), D (giao điểm của 2 đường chéo) và B (giao điểm của 2 đường thẳng chứa 2 cạnh đối) thẳng hàng nên ACHT là hình thang. (bổ đề hình thang quen thuộc)
\(\Rightarrow\) HT//AC \(\Rightarrow\) H, K, T thẳng hàng.
Lại có \(\widehat{CEH}=\widehat{CAH}\) (góc nội tiếp cùng chắn cung AH)
Mà \(\widehat{CAH}=\widehat{B}\) (cùng phụ với góc C)
\(\Rightarrow\widehat{CEH}=\widehat{B}\)
\(\Rightarrow\) Tứ giác BTEH nội tiếp \(\Rightarrow\widehat{BEH}=\widehat{BTH}\)
Mà \(\widehat{BTH}=90^o\) nên \(\widehat{BEH}=90^o\). Ta có đpcm.

C S N I M O K F A B D H
haizzz , vì mới lớp 8 nên mình chỉ làm được đến câu c, thôi , bạn thông cảm
a, Xét tam giác ABC vuông tại A và HA = HD
- Có \(\widehat{BAC}\)là góc nội tiếp đường tròn O chắn cung BC
- Mà BC là đường kính O
=> \(\widehat{BAC}=90^o\)
=> \(\Delta ABC\perp A\)
Xét \(\Delta OAD\)cân tại O ( Vì OA = OD do A , D cung thuộc O )
- Có AH là đường cao
=> OH là đường trung tuyến \(\Delta OAD\)
=> H là trug điểm AD
=> HA = HD
b, MN // SC , SC tiếp tuyến của (O)
Xét tam giác OSC có : M là trung điểm của OC
N là trung điểm của OS
=> MN là đường TB của \(\Delta OSC\)
=> MN // SC
Mà \(MN\perp OC\left(gt\right)\)
\(\Rightarrow OC\perp SC\)tại S
- Xét đường tròn O có CO là bán kính ( vì \(C\in\left(O\right)\)
\(CO\perp SC\)tại C
=> SC là tiếp tuyến của đường tròn (O)
c, BH . HC = AF . AK
Xét \(\Delta ABC\perp A\)có :
AH là đường cao
=> AH2 = BH . HC
Xét đường tròn đường kính AH có F thuộc đường tròn
\(\Rightarrow\widehat{AFH}=90^o\)
\(\Rightarrow HF\perp AK\)tại F
Xét tam giác AHK vuông tại H , ta có :
HF là đường cao
=> AH2 = AF . AK
=> BH . HC = AF . AK ( = AH2 )

a, ta có: góc AEI = 90o (góc nội tiếp chắn nửa đường tròn) => EI\(\perp\)AK tại E và AH\(\perp\)KI tại H (gt)
chúng cắt nhau tại B => B là trực tâm. => KB vuông góc AI (đpm)
b, ta có: góc ECA = góc EBA ( cùng chắn cung AE) mà góc EBA= góc HBI (hai góc đối đỉnh) (4)
ta lại có: góc HBI + góc HIB =90o (tổng 3 góc trong một tam giác) (3)
=> góc ECA + góc HIB = 90o (1)
Xét tam giác CEI vuông tại E nên: góc EKI + góc HIB =90o (2)
Từ (1) và (2) => góc ECA = góc EKI
=> tứ giác EKNC là tứ giác nội tiếp ) (đpcm)
c,Ta có: góc EAB + góc EBA = 90o và từ (3), (4) => góc EAB = góc BIH
mà góc EAB = góc BEN ( bằng 1/2 sđ cung EB)
=> góc BIH = góc BEN=> tam giác ENI cân tại N=> EN =NI (*)
Tương tự, ta có góc K + góc KAH = 90o
góc KEN + góc NEB =90o mà góc KAH = góc NEB (c.m.t) => góc KEN = góc K => tam giác KNE cân tại N => NK = NE (**)
từ (*) và (**) => NK = NI hay N là trung điểm KI ( đpcm)