Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a,
Xét Δ AHB và Δ CAB, có :
\(\widehat{AHB}=\widehat{CAB}=90^o\)
\(\widehat{ABH}=\widehat{CBA}\) (góc chung)
=> Δ AHB ∾ Δ CAB (g.g)
=> \(\dfrac{AH}{CA}=\dfrac{HB}{AB}\)
=> \(\dfrac{AB}{CA}=\dfrac{HB}{AH}\)
Xét Δ AHB và Δ CHA, có :
\(\widehat{AHB}=\widehat{CHA}=90^o\)
\(\dfrac{AB}{CA}=\dfrac{HB}{AH}\) (cmt)
=> Δ AHB ∾ Δ CHA (g.g)
=> \(\dfrac{AH}{CH}=\dfrac{HB}{HA}\)
=> \(AH^2=HB.CH\)
b, Ta có : \(AH^2=BH.CH\) (cmt)
=> \(AH^2=4.9\)
=> \(AH^2=36\)
=> AH = 6
Xét Δ AHB, có :
\(AB^2=AH^2+BH^2\)
=> \(AB^2=6^2+4^2\)
=> \(AB^2=52\)
=> AB = 7,2 (cm)
Xét Δ AHC, có :
\(AC^2=AH^2+CH^2\)
=> \(AC^2=6^2+9^2\)
=> \(AC^2=117\)
=> AC = 10,8 (cm)
Xét Δ ABC, có :
\(BC^2=AB^2+AC^2\)
=> \(BC^2=7,2^2+10,8^2\)
=> \(BC^2=168,48\)
=> BC = 12,9 (cm)
Ta có : MC = \(\dfrac{1}{2}BC\) (M là trung điểm BC do có đường trung tuyến AM)
=> MC = 6,45 (cm)
Ta có : BC = BH + HM + MC
=> 12,9 = 4 + HM + 6,45
=> HM = 12,9 - 4 - 6,45
=> HM = 2,45 (cm)
Xét Δ AMH vuông tại H, có :
\(S_{\Delta AMH}=\dfrac{1}{2}AH.HM\)
=> \(S_{\Delta AMH}=\dfrac{1}{2}.6.2,45\)
=> \(S_{\Delta AMH}=7,35\left(cm\right)\)

A B C H
chỉnh đề câu a) c/m: AH2 = BH.CH
a) Xét tam giác AHB và tam giác CHA có:
góc AHB = góc CHA = 900
góc BAH = góc ACH (cùng phụ góc HAC)
suy ra: tam giác AHB ~ tam giác CHA (g.g)
=> \(\frac{AH}{CH}=\frac{HB}{AH}\) => AH2 = HB.CH
b) CH = BC - BH = 13 - 4 = 9
Áp dụng câu a) ta có: \(AH^2=HB.CH\)
\(\Rightarrow\)\(AH=\sqrt{HB.CH}=\sqrt{4.9}=6\)

a.
Xét hai tam giác vuông HBA và ABC có:
\(\left\{{}\begin{matrix}\widehat{HBA}\text{ chung}\\\widehat{AHB}=\widehat{BAC}=90^0\end{matrix}\right.\)
\(\Rightarrow\Delta HBA\sim\Delta ABC\left(g.g\right)\)
b.
Áp dụng định lý Pitago:
\(BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10\left(cm\right)\)
Do \(\Delta HBA\sim\Delta ABC\left(cmt\right)\Rightarrow\dfrac{AH}{AC}=\dfrac{AB}{BC}\)
\(\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{6.8}{10}=4,8\left(cm\right)\)
Áp dụng định lý Pitago trong tam giác vuông HBA:
\(BH=\sqrt{AB^2-AH^2}=\sqrt{6^2-4,8^2}=3,6\left(cm\right)\)

a) Xét ΔAHB vuông tại H và ΔCAB vuông tại A có
\(\widehat{B}\) chung
Do đó: ΔAHB∼ΔCAB(g-g)
Suy ra: \(\dfrac{AB}{CB}=\dfrac{HB}{AB}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(AB^2=BH\cdot BC\)(đpcm)
b) Ta có: BC=BH+HC(H nằm giữa B và C)
nên BC=4+9=13(cm)
Ta có: \(AB^2=BH\cdot BC\)(cmt)
\(\Leftrightarrow AB^2=4\cdot13\)
hay \(AB=2\sqrt{13}\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2=13^2-\left(2\sqrt{13}\right)^2=117\)
hay \(AC=3\sqrt{13}\left(cm\right)\)
a)
Trong tam giác ABC có :
\(AH^2=BH.CH=4.9=36\Rightarrow AH=6\left(cm\right)\)
Áp dụng Pitago trong tam giác AHB vuông tại H ta có :
\(AB^2=AH^2+BH^2=6^2+4^2=52=BH.BC=4\left(9+4\right)\)
(đpcm)
b)
\(AB=\sqrt{52}=2\sqrt{13}\left(cm\right)\)
\(AC=\sqrt{BC^2-AB^2}=\sqrt{13^2-52}=3\sqrt{13}\)

a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
Do đó:ΔABC\(\sim\)ΔHBA
b: Xét ΔHBA vuông tại H và ΔHAC vuông tại H có
\(\widehat{HBA}=\widehat{HAC}\)
Do đó:ΔHBA\(\sim\)ΔHAC
c: \(BH=\sqrt{15^2-12^2}=9\left(cm\right)\)
\(BC=\dfrac{AB^2}{BH}=\dfrac{15^2}{9}=25\left(cm\right)\)
\(AC=\sqrt{25^2-15^2}=20\left(cm\right)\)
d: ta có: ΔHBA\(\sim\)ΔHAC
nên HB/HA=HA/HC
hay \(HA^2=HB\cdot HC\)

a) Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{B}\) chung
Do đó: ΔABC\(\sim\)ΔHBA(g-g)

a, Xét Δ ABC và Δ CBH
Ta có : \(\widehat{ACB}=\widehat{CHB}=90^o\)
\(\widehat{ABC}=\widehat{CBH}\) (góc chung)
=> Δ ABC ∾ Δ CBH (g.g)
b, Ta có : Δ ABC ∾ Δ CBH (cmt)
=> \(\dfrac{AB}{CB}=\dfrac{BC}{BH}\)
=> \(BC^2=AB.BH\)
c,
Ta có : AB = AH + HB
=> AB = 4 + 9
=> AB = 13 (cm)
Ta có : \(BC^2=AB.BH\left(cmt\right)\)
=> \(BC^2=13.9\)
=> \(BC^2=117\)
=> BC = 10,8 (cm)
Xét Δ ABC
Ta có : \(AB^2=AC^2+BC^2\)
=> \(13^2=AC^2+10,8^2\)
=> \(169=AC^2+116,64\)
=> \(169-116,64=AC^2\)
=> \(52,36=AC^2\)
=> AC = 7,2 (cm)
Xét Δ ABC vuông tại C
=> \(S_{\Delta ABC}=\dfrac{AC.BC}{2}\)
=> \(S_{\Delta ABC}=\dfrac{7,2.10,8}{2}\)
=> \(S_{\Delta ABC}=38,88\left(cm^2\right)\)

1: Xet ΔABH vuông tại H và ΔCAH vuông tại H có
góc ABH=góc CAH
=>ΔABH đồng dạng với ΔCAH
=>HA/HC=HB/HA
=>HA^2=HB*HC
2: AH=căn 4*9=6cm
AB=căn 4*13=2*căn 13(cm)
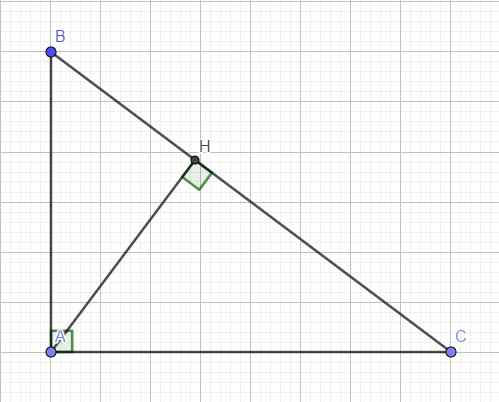
Xét tam giác ABC có đường cao AH:
+) Xét tam giác AHB vuông tại H có:
\(AB=\sqrt{AH^2+BH^2}=\sqrt{4^2+2^2}=2\sqrt{5}\left(cm\right)\) (pytago)
+) Xét tam giác AHC vuông tại H có:
\(AC=\sqrt{AH^2+HC^2}=\sqrt{4^2+8^2}=4\sqrt{5}\left(cm\right)\) (pytago)
Từ trên có: \(AB^2+AC^2=\left(2\sqrt{5}\right)^2+\left(4\sqrt{5}\right)^2=100\left(cm\right)\) (1)
Mặt khác: \(BC=BH+HC=2+8=10\left(cm\right)\Rightarrow BC^2=10^2=100\left(cm\right)\) (2)
Từ (1), (2) có: \(AB^2+AC^2=BC^2\)
=> Tam giác ABC vuông tại A (theo đl pytago đảo).