Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

số đo các góc A,B,C lần lượt tỉ lệ với 3; 2; 1
=> A/3 = B/2 = C/1
=> (A+B+C)/(3+2+1) = A/3 = B/2 = C/1
A + B + C = 180
=> 180/6 = 30 = A/3 = B/2 = C/1
=> A = 30.3 = 90
B = 30.2 = 60
C = 30
a)XÉT\(\Delta ABC\)CÓ
\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\left(Đ/L\right)\)
gọi các GÓC A,B,C LẦN LƯỢT LÀ a,b,c TỈ LỆ VỚI 3;2;1
\(\Rightarrow a:b:c=3:2:1\)
\(\Rightarrow\frac{a}{3}=\frac{b}{2}=\frac{c}{1}\)và \(a+b+c=180\)
theo tính chất dãy tỉ số bằng nhau có
\(\frac{a}{3}=\frac{b}{2}=\frac{c}{1}=\frac{a+b+c}{3+2+1}=\frac{180}{6}=30\)
do đó \(\frac{a}{3}=30\Rightarrow a=3.30=90\)
\(\frac{b}{2}=30\Rightarrow b=2.30=60\)
\(\frac{c}{1}=30\Rightarrow c=1.30=30\)
vậy \(\widehat{A}=90^0;\widehat{B}=60^o;\widehat{C}=30^o\)

Lời giải:
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\frac{\widehat{A}}{1}=\frac{\widehat{B}}{2}=\frac{\widehat{C}}{3}=\frac{\widehat{A}+\widehat{B}+\widehat{C}}{1+2+3}=\frac{180^0}{6}=30^0\) (định lý tổng 3 góc trong tam giác)
\(\Rightarrow \widehat{A}=30^0; \widehat{B}=2.30^0=60^0; \widehat{C}=3.30^0=90^0\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{1}=\dfrac{b}{2}=\dfrac{c}{3}=\dfrac{a+b+c}{1+2+3}=\dfrac{180}{6}=30\)
Do đó: a=30; b=60; c=90

Do các cạnh a, b, c tỉ lệ với 3;4;5 nên:
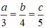
Mà chu vi tam giác ABC bằng 24 cm nên a+ b +c = 24
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
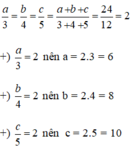
Vậy độ dài ba cạnh của tam giác ABC là 6cm,8cm và 10cm.

4) ti lê canh huyen la: 52 + 122 = 132
ta có AB/5 =AC/12 = BC/13 =>AB=20;AC=48;BC=52
5) cac canh bang 20;48 ;52
la tg vuong vi 522 = 482+202.
( giai toan giup bạn )