Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

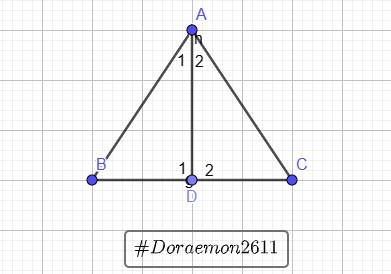
a) Xét \(\Delta ADB\) và \(\Delta ADC\) ta có:
\(\widehat{BAD}+\widehat{B}+\widehat{BDA}=180^o\)
\(\widehat{DAC}+\widehat{C}+\widehat{CDA}=180^o\)
Mà \(\widehat{B}=\widehat{C}\left(gt\right)\)(*)
\(\widehat{BAD}=\widehat{DAC}\) (AD là phân giác)
\(\Rightarrow\widehat{BDA}=\widehat{CDA}\) (**)
AD là cạnh chung. (***)
Vậy: từ (*) (**) (***) ta có \(\Delta ADB\) = \(\Delta ADC\) (g.c.g)
b) Vì: \(\Delta ADB\) = \(\Delta ADC\) (cm a)
\(\Rightarrow AB=AC\) (2 cạnh tương ứng)
c) Vì: \(\Delta ADB\) = \(\Delta ADC\) (cm a)
\(\Rightarrow DB=DC\) (2 cạnh tương ưng)
Mà D thuộc BC (gt)
=> D là trung điểm của BC. (****)
Lại có: AD là tia phân giác góc A (*****)
Từ (****) và (*****) suy ra AD là đường trung trực của BC

a) Áp dụng định lí Pytago vào tam giác ABC vuông tại A, ta có:
BC2= AB2 +AC2
=> BC =\(\sqrt{AB^2+AC^2}\)=\(\sqrt{5^2+12^2}\)=13 (cm)
Trả lời (Tự vẽ hình)
a) \(\Delta ABC\)vuông tại A
=> Áp dụng định lý Pi-ta-go
Ta có: \(BC^2=AB^2+AC^2\)
\(\Rightarrow BC^2=5^2+12^2\)
\(\Rightarrow BC^2=169\)
\(\Rightarrow BC=13\left(cm\right)\)
Vậy BC=13 (cm)
b) Xét \(\Delta ABC\&\Delta ADC\)có:
AC chung (1)
\(\widehat{BAC}\)\(=\widehat{CDA}\)\(\left(=90^o\right)\left(2\right)\)
\(AB=AD\left(gt\right)\left(3\right)\)
(1)(2)(3)\(\Rightarrow\Delta ABC=\Delta ADC\)
Vậy \(\Delta ABC=\Delta ADC\left(đpcm\right)\)
c) Vì \(\Delta ABC=\Delta ADC\)
\(\Rightarrow\hept{\begin{cases}c_1=c_2\left(cmt\right)\\BC=AE\left(gt\right)\\CEA=c_1\end{cases}\Rightarrow\Delta AEC}\)cân
Vậy \(\Delta AEC\)cân (đpcm)
\(\)

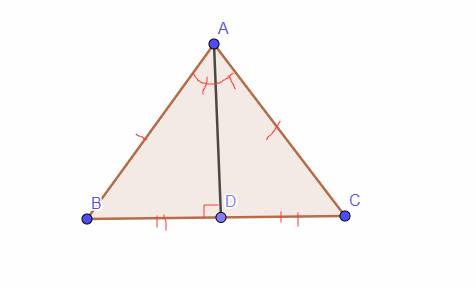
`a)` Vì `D` là trung điểm `BC=>DB=DC`
Xét `\triangle ABD` và `\triangle ACD` có:
`{:(AB=AC),(AD\text{ là cạnh chung}),(BD=CD):}}=>\triangle ABD=\triangle ACD` (c-c-c)
`b)` Vì `D` là tđ của `BC=>AD` là đường trung tuyến trong `\triangle ABC` cân tại `A`
`=>AD` đồng thời là đường phân giác của `\triangle ABC`
`=>AD` là tia phân giác của `\hat{BAC}`
`c)` Vì `D` là tđ của `BC=>AD` là đường trung tuyến trong `\triangle ABC` cân tại `A`
`=>AD` đồng thời là đường cao của `\triangle ABC`
`=>AD \bot BC`
`a,` Xét Tam giác `ABD` và Tam giác `ACD` có (bạn lưu ý ghi đúng tên của Tam giác để có các cạnh và góc tương ứng nhé)
`AB = AC (g``t)`
AD chung
`DB = DC (g``t)`
`=>` Tam giác `ABD =` Tam giác `ACD (c-c-c)`
`b,` Vì Tam giác `ABD =` Tam giác `ACD (a)`
`=>` \(\widehat{BAD}=\widehat{CAD}\) (2 góc tương ứng)
`=> AD` là tia phân giác của \(\widehat{BAC}\)
`c,` Vì Tam giác `ABD =` Tam giác `ACD (a)`
`=>` \(\widehat{ADB}=\widehat{ADC}\) (2 góc tương ứng)
Mà 2 góc này ở vị trí kề bù
`=>`\(\widehat{ADB}+\widehat{ADC}=180^0\)
`=>` \(\widehat{ADB}=\widehat{ADC}=\) \(\dfrac{180}{2}=90^0\)
`=>`\(AD\perp BC\) `(đpcm)`

a) Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2=BC^2-AB^2=5^2-3^2=16\)
hay AC=4(cm)
Vậy: AC=4cm
b)Xét ΔADC vuông tại A và ΔABC vuông tại A có
CA chung
AD=AB(gt)
Do đó: ΔADC=ΔABC(hai cạnh góc vuông)
c) Xét ΔEMD và ΔBMC có
\(\widehat{EDM}=\widehat{BCM}\)(hai góc so le trong, ED//BC)
MD=MC(M là trung điểm của CD)
\(\widehat{EMD}=\widehat{BMC}\)(hai góc đối đỉnh)
Do đó: ΔEMD=ΔBMC(g-c-g)
Suy ra: ED=BC(hai cạnh tương ứng)
mà BC=CD(ΔCDA=ΔCBA)
nên ED=CD
hay ΔCDE cân tại D

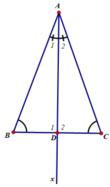

A B C D
a, Xét \(\Delta ADB;\Delta ADC\) có :
\(\left\{{}\begin{matrix}AB=AC\\DB=DC\\ADchung\end{matrix}\right.\)
\(\Leftrightarrow\Delta ADB=\Delta ADC\left(c-c-c\right)\)
b, \(\Delta ADB=\Delta ADC\left(cmt\right)\)
\(\Leftrightarrow\widehat{BDA}=\widehat{ADC}\)
Lại có :
\(\widehat{BDA}+\widehat{ADC}=180^0\left(kềbuf\right)\)
\(\Leftrightarrow\widehat{BDA}+\widehat{ADC}=\dfrac{180^0}{2}=90^0\)
\(\Leftrightarrow AD\perp BC\)