Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

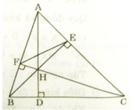
a) Xét ΔAEB và ΔAFC có:
∠AEB = ∠AFC = 90o (gt)
∠A chung
Vậy ΔAEB ∼ ΔAFC (g.g)
![]()
b) Xét ΔAEF và ΔABC có
∠A chung
AF.AB = AE.AC (Cmt)
⇒ ΔAEF ∼ ΔABC (c.g.c)
⇒ ∠AEF = ∠ABC
c) ΔAEF ∼ ΔABC (cmt)

![]()
![]()
![]()
![]()
![]()
![]()
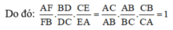

c) xét tam giác CFA và tam giác CEH có
C chung
F=E=90 độ
vậy tam giác CFA~CEH(g.g)
\(\Rightarrow\frac{CF}{CE}=\frac{CA}{CH}\Rightarrow\frac{CF}{CA}=\frac{CE}{CH}\).
xét tam giác CFE và CAH có
C chung
\(\frac{CF}{CA}=\frac{CE}{CH}\left(cmt\right)\)
vậy chúng đồng dạng với nhau.
suy ra góc CFE=CAH(góc tương ứng)
mà DFH=CAH( do tam giác FHD~AHC)
từ hai điều đó suy ra CFE=DFH
hay CFE=CFD
vậy FC là tia phân giác góc DFE( điều phải chứng minh)
xog rồi bạn

b) Xét tứ giác BFHD có
\(\widehat{BFH}+\widehat{BDH}=180^0\)
nên BFHD là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Suy ra: \(\widehat{FBH}=\widehat{FDH}\)(hai góc nội tiếp cùng chắn cung FH)
hay \(\widehat{ABE}=\widehat{FDH}\)(1)
Xét tứ giác CDHE có
\(\widehat{CDH}+\widehat{CEH}=180^0\)
nên CDHE là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Suy ra: \(\widehat{HDE}=\widehat{ECH}\)(Hai góc nội tiếp cùng chắn cung EH)
hay \(\widehat{HDE}=\widehat{ACF}\)(2)
Xét ΔABE vuông tại E và ΔACF vuông tại F có
\(\widehat{FAC}\) chung
Do đó: ΔABE\(\sim\)ΔACF(g-g)
Suy ra: \(\widehat{ABE}=\widehat{ACF}\)(3)
Từ (1), (2) và (3) suy ra \(\widehat{FDH}=\widehat{EDH}\)
hay DH là tia phân giác của \(\widehat{EDF}\)