Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có :
M + N = 6x2 + 3xy - 2y2 + ( 3y2 - 2x2 - 3xy )
= 6x2 + 3xy - 2y2 + 3y2 - 2x2 - 3xy
= 4x2 + y2 ( đoạn này mình làm hơi tắt sry nha)
Do 4x2 + y2 \(\ge\)0
Suy ra : M + N \(\ge\) 0 <=> M và N \(\ge\)0
Do đó không tồn tại giá trị nào của x để 2 đa thức M và N có cùng giá trị âm
Đặt \(X=M+N=4x^2+y^2\)
Vì \(4x^2\ge0\forall x\)
\(y^2\ge0\forall x\)
\(X\ge0\forall x\)
Vậy...

a: \(A=6x^2+9xy-y^2-5x^2+2y=x^2+9xy-y^2+2y\)
b: \(P=x^2-7xy+8y^2+3xy-4y^2=x^2-4xy+4y^2\)
\(P=25x^2y-13xy^2+y^3-11x^2y+2y^3=14x^2y-13xy^2+3y^3\)

Cộng hai đa thức P và Q, ta được kết quả: P+Q= 2x2+3y2 (phần này mình chỉ ghi kq thoy, rõ àng thì bạn tự làm nhé ^^)
Ta thấy rằng: 2x2 ≥0 ; 3y2≥0 => 2x2+3y2 ≥ 0 hay P+Q≥0
Vậy hai đa thức P và Q không thể cùng có giá trị âm

Ko ghi đề nha! Gấp nên tắt nha!![]()
* \(A=\left(6x^2+9xy-y^2\right)-\left(5x^2-2y\right)\)
\(A=6x^2+9xy-y^2-5x^2+2y\)
⇒\(A=x^2+9xy-y^2+2y\)
*+\(P=\left(x^2-7xy+8y^2\right)+\left(3xy-4y^2\right)\)
\(P=x^2-7xy+8y^2+3xy-4y^2\)
⇒\(P=x^2-4xy+4y^2\)
+ \(P=\left(25x^2y-13xy^2+y^3\right)-\left(11x^2y-2y^3\right)\)
\(P=25x^2-13xy^2+y^3-11x^2y+2y^3\)
⇒\(P=25x^2-13xy^2+3y^3-11x^2y\)
Xin lỗi do ko on nhưng 1 kick nhé
muốn cộng trứ 2 đa thức ta cần:
B1: Viết phép cộng 2 đa thức, mỗi đa thức được đặt trong một dấu ngoặc
B2: Áp dụng quy tắc dấu ngoặc
B3: Áp dụng tính chất giao hoán và kết hợp để nhóm các hạng tử đồng dạng
B4: Cộng trừ các đơn thức đồng dạng
A +(5x2_2y)= 6x2+9xy-y2
A+5x2-2y=6x2+9xy-y2
A =(6x2+9xy-y2)-(5x2+2y)
A =6x2+9xy-y2-5x2-2y
A =(6x2-5x2)+(-y2+y2)+9xy-5x2
A =x2+9xy-5x2
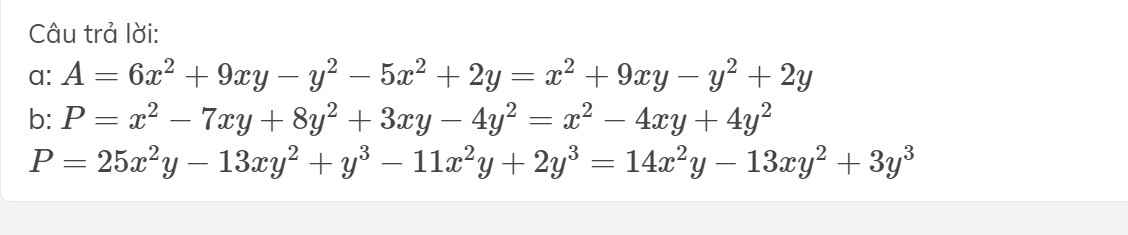
\(M+N=\left(2x^2+3xy+2y^2\right)+\left(-5x^2-3xy+2y^2+5\right)\\ =2x^2+3xy+2y^2-5x^2-3xy+2y^2+5\\ =-3x^2+4y^2+5\\ M-N=\left(2x^2+3xy+2y^2\right)-\left(-5x^2-3xy+2y^2+5\right)\\ =2x^2+3xy+2y^2+5x^2+3xy-2y^2-5\\ =7x^2+6xy-5\)
\(N-M=\left(-5x^2-3xy+2y^2+5\right)-\left(2x^2+3xy+2y^2\right)\\ =-5x^2-3xy+2y^2+5-2x^2-3xy-2y^2\\ =-7x^2-6xy+5\)