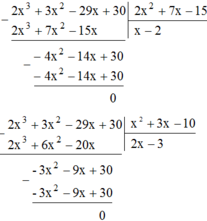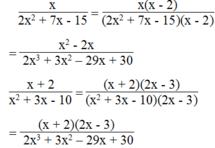Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Ta có: \(\frac{2}{2x^2+7x-15}=\frac{2}{x(2x-3)+5(2x-3)}=\frac{2}{(2x-3)(x+5)}\)
\(\frac{x}{x^2+3x-10}=\frac{x}{x^2+5x-2x-10}=\frac{x}{x(x+5)-2(x+5)}=\frac{x}{(x-2)(x+5)}\)
Do đó khi quy đồng thì mẫu thức chung của 2 phân số này là:
\((x+5)(2x-3)(x-2)=2x^3+3x^2-29x+30\)
Ta có đpcm.

Bài 1:
a: \(=\dfrac{3x+5-5}{2x}=\dfrac{3x}{2x}=\dfrac{3}{2}\)
b: \(=\dfrac{2x}{x+3}\cdot\dfrac{\left(x+3\right)\left(x-3\right)}{x}=2\left(x-3\right)\)
Bài 2:
=>x^3+x+2x^2+2+a-2 chia hết cho x^2+1
=>a-2=0
=>a=2

C1
a) -7x(3x-2)=-21x^2+14x
b) 87^2+26.87+13^2=87^2+2.13.87+13^2=(87+13)^2=100^2
C2
a) (x-5)(x+5)
b)3x(x+5)-2(x+5)=(3x-2)(x+5)=0
\(\Rightarrow\left[\begin{array}{nghiempt}3x-2=0\\x+5=0\end{array}\right.\)
\(\Rightarrow\left[\begin{array}{nghiempt}x=\frac{2}{3}\\x=-5\end{array}\right.\)
Vậy S={-5;2/3}
C3:
a)3x^3-2x^2+2=(x+1)(3x^2-5x-5)-3
b) Để A chia hết cho B=> x+1\(\inƯ\left(-3\right)\)
\(\Rightarrow\begin{cases}x+1=3\\x+1=-3\\x+1=1\\x+1=-1\end{cases}\)\(\Rightarrow\begin{cases}x=2\\x=-4\\x=0\\x=-2\end{cases}\)