Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(A\left(x\right)+B\left(x\right)=4x^5-2x^2-1\)
\(\Rightarrow2x^4-3x^3-4x+\dfrac{1}{2}+B\left(x\right)=4x^5-2x^2-1\)
\(\Rightarrow B\left(x\right)=4x^5-2x^2-1-2x^4+3x^3+4x-\dfrac{1}{2}\)
\(\Rightarrow B\left(x\right)=4x^5-2x^4+3x^3-2x^2+4x-\dfrac{3}{2}\)
b) \(A\left(x\right)-C\left(x\right)=2x^3\)
\(\Rightarrow2x^4-3x^3-4x+\dfrac{1}{2}-C\left(x\right)=2x^3\)
\(\Rightarrow C\left(x\right)=2x^4-3x^3-4x+\dfrac{1}{2}-2x^3\)
\(\Rightarrow C\left(x\right)=2x^4-3x^3-2x^3-4x+\dfrac{1}{2}\)
\(\Rightarrow C\left(x\right)=2x^4-5x^3-4x+\dfrac{1}{2}\)
a) B(x) = 4x5 -2x2 -1 - A(x) = 4x5 -2x2 -1 -2x4 +3x3+4x -1/2
B(x) = 4x5 -2x4 +3x3-2x2 +4x - 1/2
b) tt

bài 1:
a) C= 0
hay 3x+5+(7-x)=0
3x+(7-x)=-5
với 3x=-5
x= -5:3= \(x = { {-5} \over 3}\)
với 7-x=-5
x= 7+5= 12
=> nghiệm của đa thức C là: x=\(x = { {-5} \over 3}\) và x= 12
mình làm một cái thui nhá, còn đa thức D cậu lm tương tự nha

a) Ta có : \(C\left(x\right)+B\left(x\right)=A\left(x\right)\)
\(\Leftrightarrow C\left(x\right)=A\left(x\right)-B\left(x\right)\)
\(=x^5+3x^4-2x^3-9x^2+11x-6-\left(x^5+3x^4-2x^3-x-8\right)\)
\(=x^5+3x^4-2x^3-9x^2+11x-6-x^5-3x^4+2x^3+x+8\)
\(=-9x^2+12x+2\)
b) Ta có : \(C\left(x\right)=2x+2\)
\(\Leftrightarrow-9x^2+12x+2=2x+2\)
\(\Leftrightarrow\) \(-9x^2+10x=0\)
\(\Leftrightarrow\) \(x\left(-9x+10\right)=0\)
\(\Leftrightarrow\)\(\orbr{\begin{cases}x=0\\x=\frac{10}{9}\end{cases}}\)
c) Giả sử : \(C\left(x\right)=2012\)
\(\Leftrightarrow\)\(-9x^2+12x+2=2012\)
\(\Leftrightarrow-9x^2+12x-2010=0\)
\(\Leftrightarrow\)\(9x^2-12x+2010=0\)
\(\Leftrightarrow\left(9x^2-2.3x.2+4\right)+2006=0\)
\(\Leftrightarrow\left(3x-2\right)^2+2006=0\)(vô nghiệm vì \(\left(3x-2\right)^2\ge0\forall x\inℝ\))
Do đó với x nguyên thì C(x) không thể nhận giá trị bằng 2012.

3) tìm m để x = -1 là nghiệm của đa thức M(x) = x^2 - mx +2
\(\Rightarrow M\left(x\right)=x^2-mx+2\)
\(\Leftrightarrow\left(-1\right)^2-m\left(-1\right)+2=0\)
\(\Leftrightarrow1-m\left(-1\right)=-2\)
\(\Leftrightarrow m\left(-1\right)=3\)
\(\Leftrightarrow m=-3\)
vậy với m = -3 thì x= -1 là nghiệm của đa thức M(x)
4) \(K\left(x\right)=a+b\left(x-1\right)+c\left(x-1\right)\left(x-2\right)\)
\(\Leftrightarrow K\left(1\right)=a+b\left(1-1\right)+c\left(1-1\right)\left(1-2\right)=1\)
\(\Leftrightarrow a=1\)
\(\Leftrightarrow K\left(2\right)=a+b\left(2-1\right)+c\left(2-1\right)\left(2-2\right)=3\)
\(\Leftrightarrow K\left(2\right)=a+b=3\)
\(\Leftrightarrow K\left(0\right)=a+b\left(0-1\right)+c\left(0-1\right)\left(0-2\right)=5\)
\(\Leftrightarrow a+\left(-b\right)+c2=5\)
ta có \(\hept{\begin{cases}a=1\\a+b=3\\a+\left(-b\right)+c2=5\end{cases}}\Leftrightarrow\hept{\begin{cases}a=1\\1+b=3\\1+\left(-b\right)+c2=5\end{cases}}\Leftrightarrow\hept{\begin{cases}a=1\\b=2\\-1+c2=5\end{cases}}\Leftrightarrow\hept{\begin{cases}a=1\\b=2\\c2=6\end{cases}}\Leftrightarrow\hept{\begin{cases}a=1\\b=2\\c=3\end{cases}}\)
vậy \(a=1;b=2;c=3\)
1. a) Sắp xếp :
f(x) = -x5 - 7x4 - 2x3 + x4 + 4x + 9
g(x) = x5 + 7x4 + 2x3 + 2z2 - 3x - 9
b) h(x) = f(x) + g(x)
= -x5 - 7x4 - 2x3 + x2 + 4x + 9 + x5 + 7x4 + 2x3 + 2x2 - 3x - 9
= ( x5 - x5 ) + ( 7x4 - 7x4 ) + ( 2x3 - 2x3 ) + ( 2x2 + x2 ) - 3x + ( 9 - 9 )
= 3x2- 3x
c) h(x) có nghiệm <=> 3x2 - 3x = 0
<=> 3x( x - 1 ) = 0
<=> 3x = 0 hoặc x - 1 = 0
<=> x = 0 hoặc x = 1
Vậy nghiệm của h(x) là x= 0 hoặc x = 1
2. D(x) = A(x) + B(x) - C(x)
= 6x3 + 5x2 + x3 - x2 - ( -2x3 + 4x2 )
= 6x3 + 5x2 + x3 - x2 + 2x3 - 4x2
= ( 6x3 + x3 + 2x3 ) + ( 5x2 - x2 - 4x2 )
= 9x3
b) D(x) có nghiệm <=> 9x3 = 0 => x = 0
Vậy nghiệm của D(x) là x = 0
3. M(x) = x2 - mx + 2
x = -1 là nghiệm của M(x)
=> M(-1) = (-1)2 - m(-1) + 2 = 0
=> 1 + m + 2 = 0
=> 3 + m = 0
=> m = -3
Vậy với m = -3 , M(x) có nghiệm x = -1
4. K(x) = a + b( x - 1 ) + c( x - 1 )( x - 2 )
K(1) = 1 => a + b( 1 - 1 ) + c( 1 - 1 )( 1 - 2 ) = 1
=> a + 0b + c.0.(-1) = 1
=> a + 0 = 1
=> a = 1
K(2) = 3 => 1 + b( 2 - 1 ) + c( 2 - 1 )( 2 - 2 ) = 3
=> 1 + 1b + c.1.0 = 3
=> 1 + b + 0 = 3
=> b + 1 = 3
=> b = 2
K(0) = 5 => 1 + 5( 0 - 1 ) + c( 0 - 1 )( 0 - 2 ) = 5
=> 1 + 5(-1) + c(-1)(-2) = 5
=> 1 - 5 + 2c = 5
=> 2c - 4 = 5
=> 2c = 9
=> c = 9/2
Vậy a = 1 ; b = 2 ; c = 9/2

Theo bài ra ta có :
\(A\left(x\right)+B\left(x\right)=6x^5-x^2+1\)
\(2x^4-3x^3+3-5x+B\left(x\right)=6x^5-x^2+1\)
\(B\left(x\right)=6x^5-x^2+1-2x^4+3x^3-3+5x\)
\(B\left(x\right)=6x^5-x^2-2-2x^4+3x^3+5x\)

a) D(x) = 2x2 + 3x - 35
D(-5) = 2 . ( -5 )2 + 3 . ( -5 ) -35 = 2 . 25 - 15 - 35 = 50 - 15 - 35 = 0
=> x = -5 là nghiệm của D(x)
b) F(x) = -5x - 6
F(x) = 0 <=> -5x - 6 = 0
<=> -5x = 6
<=> x = -6/5
c) E - ( 2x2 - 5xy2 + 3y3 ) = 5x2 + 6xy2 - 8y3
E = 5x2 + 6xy2 - 8y3 + 2x2 - 5xy2 + 3y3
E = 7x2 + xy2 -5y3
a, \(D\left(x\right)=2x^2+3x-35\)
\(D\left(-5\right)=2\left(-5\right)^2+3.\left(-5\right)-35=2.25-15-35=0\)
Vậy x = -5 là nghiệm của đa thức
b, Sửa đề \(F\left(x\right)=-5x-6=0\)
\(x=-\frac{6}{5}\)
c, \(E-\left(2x^2-5xy^2+3y^3\right)=5x^2+6xy^2-8y^3\)
\(E-2x^2+5xy^2-3y^3=5x^2+6xy^2-8y^3\)
\(E=5x^2+6xy^2-8y^3+2x^2-5xy^2+3y^3\)
\(E=7x^2+xy^2-5y^3\)

a) Vì P(x) + Q(x) = x5 – 2x2 + 1 nên
Q(x) = x5 – 2x2 + 1 – P(x)
b) Vì P(x) – R(x) = x3 nên
R(x) = P(x) – x3
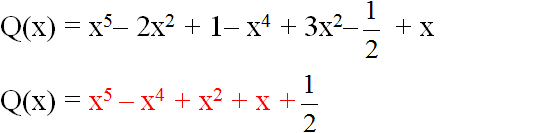
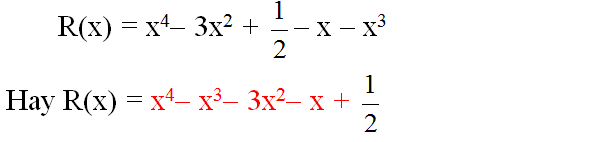
a) Ta có:
B = (A + B) – A
= (x3 + 3x + 1) – (x4 + x3 – 2x – 2)
= x3 + 3x + 1 – x4 - x3 + 2x + 2
= – x4 + (x3 – x3) + (3x + 2x) + (1 + 2)
= – x4 + 5x + 3.
b) C = A - (A – C)
= x4 + x3 – 2x – 2 – x5
= – x5 + x4 + x3 – 2x – 2.
c) D = (2x2 – 3) . A
= (2x2 – 3) . (x4 + x3 – 2x – 2)
= 2x2 . (x4 + x3 – 2x – 2) + (-3) .(x4 + x3 – 2x – 2)
= 2x2 . x4 + 2x2 . x3 + 2x2 . (-2x) + 2x2 . (-2) + (-3). x4 + (-3) . x3 + (-3). (-2x) + (-3). (-2)
= 2x6 + 2x5 – 4x3 – 4x2 – 3x4 – 3x3 + 6x + 6
= 2x6 + 2x5 – 3x4 + (-4x3 – 3x3) – 4x2+ 6x + 6
= 2x6 + 2x5 – 3x4 – 7x3 – 4x2+ 6x + 6.
d) P = A : (x+1) = (x4 + x3 – 2x – 2) : (x + 1)
Vậy P = x3 - 2
e) Q = A : (x2 + 1)
Nếu A chia cho đa thức x2 + 1 không dư thì có một đa thức Q thỏa mãn
Ta thực hiện phép chia (x4 + x3 – 2x – 2) : (x2 + 1)
Do phép chia có dư nên không tồn tại đa thức Q thỏa mãn