Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(R=x^4\left(x-2345\right)+2345x^2\left(x-1\right)+2345\left(x-1\right)\)\(=-x^4+x^2\left(x+1\right)\left(x-1\right)+\left(x-1\right)\left(x+1\right)\)\(=-x^4+x^4-x^2+x^2-1=-1\)
Coi lại giúp mình nha
\(gt\Rightarrow x+1=2345\)
\(R=x^5-\left(x+1\right)x^4+\left(x+1\right)x^3-\left(x+1\right)x^2+\left(x+1\right)x-\left(x+1\right)\)
\(R=x^5-x^5-x^4+x^4+x^3-x^3-x^2+x^2+x-x-1\)
\(R=-1\)

Lời giải:
Ta biến đổi $R$ như sau :
\(R=x^5-2344x^4-x^4+2344x^3+x^3-2344x^2-x^2+2344x+x-2344-1\)
\(=(x^5-2344x^4)-(x^4-2344x^3)+(x^3-2344x^2)-(x^2-2344x)+(x-2344)-1\)
\(=x^4(x-2344)-x^3(x-2344)+x^2(x-2344)-x(x-2344)+(x-2344)-1\)
\(=(x-2344)(x^4-x^3+x^2-x+1)-1\)
Tại $x=2344$ thì \(x-2344=0\). Do đó:
\(R=0.(x^4-x^3+x^2-x+1)-1=-1\)

\(M\left(x\right)=P\left(x\right)+Q\left(x\right)=2,5x^6-4+2,5x^5-6x^3+2x^2\)-5x+\(3x-2,5x^6-x^2+5-2,5x^5+6x^3\)
=\(\left(2,5x^6-2,5x^6\right)\)+\(\left(2,5x^5-2,5x^5\right)\)\(\left(-6x^3+6x^3\right)\)+\(\left(2x^2-x^2\right)\)+\(\left(-5x+3x\right)\)+(-4+5)
= \(x^2-2x+1\)

Bài 1:
Thay x=1 vào đa thức F(x) ta được:
F(1) = 14+2.13-2.12-6.1+5 = 0
=> x=1 là nghiệm của đa thức F(x)
Tương tự ta thế -1; 2; -2 vào đa thức F(x)
Vậy x=1 là nghiệm của đa thức F(x)

a) \(\frac{1}{2010}\)và \(\frac{-7}{19}\)
Ta có : \(\frac{1}{2010}>0>\frac{-7}{19}\)
\(\Rightarrow\frac{1}{2010}>\frac{-7}{19}\)
b)\(\frac{497}{-499}\)và \(\frac{-2345}{2341}\)
Ta có : \(\frac{497}{-499}< -1< \frac{-2345}{2341}\)
\(\Rightarrow\frac{497}{-499}>\frac{-2345}{2341}\)
c)\(\frac{2000}{2001}\)và \(\frac{2001}{2002}\)
Ta có : \(\frac{2000}{2001}=1-\frac{1}{2001};\frac{2001}{2002}=1-\frac{1}{2002}\)
mà \(\frac{1}{2001}>\frac{1}{2002}\Rightarrow1-\frac{1}{2001}< 1-\frac{1}{2002}\)
\(\Rightarrow\frac{2000}{2001}< \frac{2001}{2002}\)
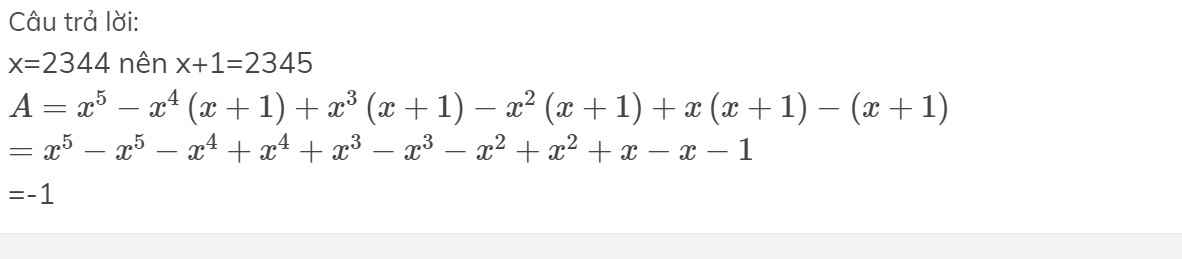
x=2344 nên x+1=2345
\(A=x^5-x^4\left(x+1\right)+x^3\left(x+1\right)-x^2\left(x+1\right)+x\left(x+1\right)-\left(x+1\right)\)
\(=x^5-x^5-x^4+x^4+x^3-x^3-x^2+x^2+x-x-1\)
=-1