Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho a',b',c' là số đo cạnh của tam giác A'B'C'
a,b,c là số đo cạnh của tam giác ABC
a) Theo đề bài ta có: \(\frac{a'}{a}=\frac{b'}{b}=\frac{c'}{c}=k=\frac{3}{5}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có: \(\frac{a'}{a}=\frac{b'}{b}=\frac{c'}{c}=\frac{a'+b'+c'}{a+b+c}=\frac{P_{A'B'C'}}{P_{ABC}}=k=\frac{3}{5}\)
Vậy tỉ số chu vi hai tam giác đã cho là 3/5
b) Chu vi tam giác ABC là: \(P_{ABC}=40:\left(5-3\right)\cdot5=100\left(dm\right)\)
Chu vi tam giác A'B'C' là: \(P_{A'B'C'}=P_{ABC}-40dm=100dm-40dm=60\left(dm\right)\)
A B C A' B' C'
a, Gọi CV tam giác A'B'C' là P', ABC là P
\(\Delta A'B'C'~\Delta ABC\)theo tỉ số đồng dạng \(k=\frac{3}{5}\)
\(\Rightarrow\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{C'A'}{CA}=\frac{3}{5}\)
Áp dụng t/c DTSBN , ta có :
\(\frac{3}{5}=\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{C'A'}{CA}\)
\(=\frac{A'B'+B'C'+C'A'}{AB+BC+CA}=\frac{P'}{P}\)
Vậy tỉ số chu vi tam giác A'B'C' và ABC là \(\frac{3}{5}\)

Hướng dẫn cách hack VIP OLM Vĩnh Viễn siêu dễ chỉ 10 phút là xong: youtube.com/watch?v=zYcnHqUcGZE&t

Toán lớp 8 thì mik nghĩ bn vào lazi.vn hoặc hoc.24h.vn để hỏi nha
~ Hok tốt ~
#JH
a)
Xét tam giác ABC ta có
\(AB^2+AC^2=BC^2\)(định lý py ta go)
144 + 256 = BC2
400 = BC2
BC = 20 ( cm )
Xét tam giác ABC có
BD là đường phân giác của tam giác
nên AD/DC = AB/BC = 16/20 = 4/5
có AD + DC = AC = 16
dễ tìm ra AD = 64/9 (cm)
DC = 80/9 (cm)
b) xét 2 tam giác HBA và ABC
có góc ABC chung
2 góc AHB và CAB bằng nhau cùng bằng 90 độ
nên 2 tam giác HAB và ABC đồng dạng với nhau
c)
có 2 tam giác HAB và ABC đồng dạng với nhau
nên \(\frac{S_{HAB}}{S_{ABC}}=\left(\frac{AB}{BC}\right)^2=\left(\frac{12}{20}\right)^2=\frac{9}{25}\)
d)
có E là hình chiếu của của C trên BD
nên \(CE\perp BD\)
suy ra \(\widehat{BEC}=90^0\)
xét 2 tam giác BHK và BEC
có \(\widehat{BHK}=\widehat{BEC}=90^0\)
\(\widehat{CEB}\)chung
nên 2 tam giác BHK và BEC đồng dạng với nhau
suy ra \(\frac{BH}{BE}=\frac{BK}{BC}\Rightarrow BH\cdot BC=BK\cdot BE\)(1)
có 2 tam giác HAB và ABC đồng dạng với nhau
suy ra \(\frac{AB}{BC}=\frac{BH}{AB}\Rightarrow AB^2=BH\cdot BC\left(2\right)\)
từ (1) và (2) suy ra
\(AB^2=BK\cdot BE\)

AB = 18; BC = 21; CA =12 (gt)
=> chu vi tg ABC là : 18 + 12 + 21 = 51
tam giác ABC ~ tam giác A'B'C' (gt)
=> AB/A'B' = AC/A'C' = BC/B'C' = C ABC/C A'B'C
=> AB/A'B' = AC/C'A' = BC/B'C' = 3/4
xong tự tính ra

ABA′B′ABA′B′ = BCB′C′BCB′C′= CAC′A′CAC′A′= 3/2
=> ∆ABC ∽ ∆A'B'C'
b) CABCCA′B′C′CABCCA′B′C′= 3/2
a)Xét \(\Delta ABC\) và \(\Delta A'B'C'\) có:
\(\dfrac{AB}{A'B'}=\dfrac{BC}{B'C'}=\dfrac{AC}{A'C'}\)
\(\Rightarrow\Delta ABC\)∽\(\Delta A'B'C'\)(c.c.c)
b)Từ câu a và áp dụng tính chất tỉ lệ thức ta có:
\(\dfrac{AB}{A'B'}=\dfrac{BC}{B'C'}=\dfrac{AC}{A'C'}=\dfrac{AB+BC+AC}{A'B'+B'C'+A'C'}=\dfrac{3}{2}\)
mà \(C_{ABC}=AB+BC+AC\)
\(C_{A'B'C'}=A'B'+B'C'+A'C'\)
Vậy tỉ số chu vi của \(\Delta ABC\) và \(\Delta A'B'C'\)là:
\(\dfrac{C_{ABC}}{C_{A'B'C'}}=\dfrac{3}{2}\)
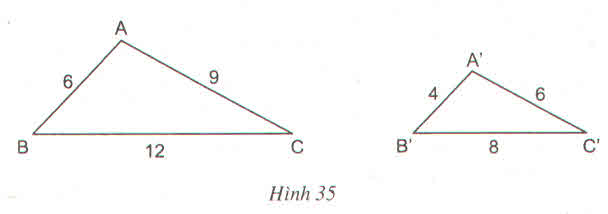
Ta có tỉ số chu vi bằng tỉ số đồng dạng nên tam có: P/P' = k = 5/9 ⇒ 9P - 5P' = 0
Mà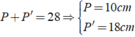
Chọn đáp án C.