Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vì \(\Delta\)ABC cân tại A
=> AB = AC và \(\widehat{ABC}\) = \(\widehat{ACB}\)
hay \(\widehat{EBM}\) = \(\widehat{ICM}\)
Xét \(\Delta\)EBM vuông tại E và \(\Delta\)ICM vuông tại I có:
BM = CM (suy từ gt)
\(\widehat{EBM}\) = \(\widehat{ICM}\) (c/m trên)
=> \(\Delta\)EBM = \(\Delta\)ICM (ch - gn)
=> EB = IC (2 cạnh t/ư)
Ta có: AE + EB = AB
AI + IC = AC
mà EB = IC; AB = AC => AE = AI
b) Gọi giao điểm của AM và EI là D.
Vì \(\Delta\)EBM = \(\Delta\)ICM (câu a)
=> EM = IM (2 cạnh t/ư)
Xét \(\Delta\)AEM và \(\Delta\)AIM có:
AE = AI (câu a)
AM chung
EM = IM (c/m trên)
=> \(\Delta\)AEM = \(\Delta\)AIM (c.c.c)
=> \(\widehat{EAM}\) = \(\widehat{IAM}\) (2 góc t/ư)
hay \(\widehat{EAD}\) = \(\widehat{IAD}\)
Xét \(\Delta\)ADE và \(\Delta\)ADI có:
AE = AI (câu a)
\(\widehat{EAD}\) = \(\widehat{IAD}\) (c/m trên)
AM chung
=> \(\Delta\)ADE = \(\Delta\)ADI (c.g.c)
\(\widehat{AEI}\) + \(\widehat{AIE}\) + \(\widehat{BAC}\) = 180o
=> 2\(\widehat{AEI}\) = 180o - \(\widehat{BAC}\)
=> \(\widehat{AEI}\) = \(\frac{180^o-\widehat{BAC}}{2}\) (3)
Do \(\Delta\)ABC cân tại A
=> \(\widehat{ABC}\) = \(\widehat{ACB}\)
Áp dụng tc tổng 3 góc trong 1 tg ta có:
\(\widehat{ABC}\) + \(\widehat{ACB}\) + \(\widehat{BAC}\) = 180o
=> 2\(\widehat{ABC}\) = 180o - \(\widehat{BAC}\)

A B C E I M D
a) Vì \(\Delta\)ABC cân tại A
=> AB = AC và \(\widehat{ABC}\) = \(\widehat{ACB}\)
hay \(\widehat{EBM}\) = \(\widehat{ICM}\)
Xét \(\Delta\)EBM vuông tại E và \(\Delta\)ICM vuông tại I có:
BM = CM (suy từ gt)
\(\widehat{EBM}\) = \(\widehat{ICM}\) (c/m trên)
=> \(\Delta\)EBM = \(\Delta\)ICM (ch - gn)
=> EB = IC (2 cạnh t/ư)
Ta có: AE + EB = AB
AI + IC = AC
mà EB = IC; AB = AC => AE = AI
b) Gọi giao điểm của AM và EI là D.
Vì \(\Delta\)EBM = \(\Delta\)ICM (câu a)
=> EM = IM (2 cạnh t/ư)
Xét \(\Delta\)AEM và \(\Delta\)AIM có:
AE = AI (câu a)
AM chung
EM = IM (c/m trên)
=> \(\Delta\)AEM = \(\Delta\)AIM (c.c.c)
=> \(\widehat{EAM}\) = \(\widehat{IAM}\) (2 góc t/ư)
hay \(\widehat{EAD}\) = \(\widehat{IAD}\)
Xét \(\Delta\)ADE và \(\Delta\)ADI có:
AE = AI (câu a)
\(\widehat{EAD}\) = \(\widehat{IAD}\) (c/m trên)
AM chung
=> \(\Delta\)ADE = \(\Delta\)ADI (c.g.c)
\(\widehat{AEI}\) + \(\widehat{AIE}\) + \(\widehat{BAC}\) = 180o
=> 2\(\widehat{AEI}\) = 180o - \(\widehat{BAC}\)
=> \(\widehat{AEI}\) = \(\frac{180^o-\widehat{BAC}}{2}\) (3)
Do \(\Delta\)ABC cân tại A
=> \(\widehat{ABC}\) = \(\widehat{ACB}\)
Áp dụng tc tổng 3 góc trong 1 tg ta có:
\(\widehat{ABC}\) + \(\widehat{ACB}\) + \(\widehat{BAC}\) = 180o
=> 2\(\widehat{ABC}\) = 180o - \(\widehat{BAC}\)
Xét \(\Delta\)ABM và \(\Delta\)ACM có:
AB = AC
\(\widehat{BAM}\) = \(\widehat{CAM}\) (tự suy ra)
AM chung
=> \(\Delta\)ABM = \(\Delta\)ACM (c.g.c)
=> \(\widehat{AMB}\) = \(\widehat{AMC}\) (2 góc t/ư)
mà \(\widehat{AMB}\) + \(\widehat{AMC}\) = 180o (kề bù)
=> \(\widehat{AMB}\) = \(\widehat{AMC}\) = 90o
Do đó AM \(\perp\) BC
=> \(\Delta\)ABM vuông tại M
Áp dụng định lý pytago vào \(\Delta\)ABM vuông tại M có:
AB2 = AM2 + BM2
=> 152 = AM2 + 92
=> AM = 12cm

tự kẻ hình nha
a) vì tam giác BEC vuông tại E=> EBC=90 độ-ECB
vì ECB+BCD= 90 độ( AC vuông góc với CD)
=> BCD=90 độ-ECB
xét tam giác HMB và tam giác CMD có
MB=MC(gt)
HMB=DMC(đối đỉnh)
HBM=MCD(= 90 độ-ECB)
=> tam giác HMB= tam giác DMC(gcg)
=> BH=CD (hai cạnh tương ứng)
b) từ tam giác HMB= tam giác DMC=> HM=DM( hai cạnh tương ứng)
=> M là trung điểm của HD
c) hình như nhầm một chút rồi, phải là AM,HO,DI giao nhau
vì M là trung điểm của HD=> AM là trung tuyến
vì O là trung điểm của AD=> HO là trung tuyến
vì I là trung điểm của AH=> DI là trung tuyến
=> AM, HO,DI giao nhau tại một điểm ( trong tam giác, 3 đường trung tuyến giao nhau tại một điểm)
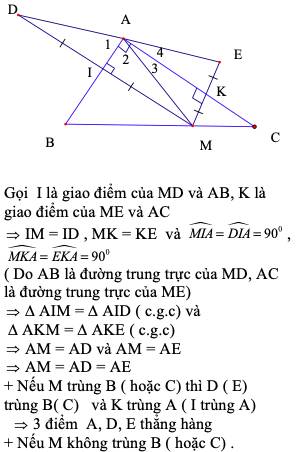
Sửa đề: ΔACB vuông tại A
a: AB là trung trực của MD
=>AM=AD
=>ΔAMD cân tạiA
=>AB là phân giác của góc MAD(1)
AC là trung trực của ME
=>AM=AE
=>ΔAME cân tại A
=>AC là phân giác của góc MAE(2)
=>AD=AE=AM
b: Từ (1) (2) suy ra góc DAE=2*góc BAC=180 độ
=>D,A,E thẳng hàng