Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D M N O câu a CHỨNG Minh AB = DC CHỨ sao AB = BC ĐC
A) XÉT \(\Delta ABC\)VÀ \(\Delta CDA\)CÓ
\(\widehat{ACB}=\widehat{CAD}\)( VÌ AD // BC , HAI GÓC NÀY Ở VỊ TRÍ SO LE TRONG )
AC LÀ CẠNH CHUNG
\(\widehat{BAC}=\widehat{DCA}\)( VÌ AB // DC , HAI GÓC NÀY Ở VỊ TRÍ SO LE TRONG )
=> \(\Delta ABC=\Delta CDA\left(g-c-g\right)\)
=> AD = BC (HAI CẠNH TƯƠNG ỨNG )
=> AB = DC ( HAI CẠNH TƯƠNG ỨNG )
TA CÓ M LÀ TRUNG ĐIỂM CỦA BC
\(\Rightarrow BM=CM=\frac{BC}{2}\left(1\right)\)
TA CÓ N LÀ TRUNG ĐIỂM CỦA AD
\(\Rightarrow AN=DN=\frac{AD}{2}\left(2\right)\)
TỪ (1) VÀ (2)
\(BM=CM=\frac{BC}{2}\)
\(AN=DN=\frac{AD}{2}\)
MÀ AD = BC ( CMT)
=> \(BM=CM=AN=DN\)
XÉT \(\Delta BAM\)VÀ \(\Delta DCN\)CÓ
\(BA=DC\)(VÌ \(\Delta ABC=\Delta CDA\))
\(\widehat{ABM}=\widehat{CDN}\)(VÌ \(\Delta ABC=\Delta CDA\))
\(BM=DN\left(cmt\right)\)
=>\(\Delta BAM=\Delta DCN\left(c-g-c\right)\)
=> AM = CN (HAI CẠNH TƯƠNG ỨNG )
c) XÉT TỨ GIÁC ABCD
ta có \(AD=BC\left(cmt\right);AB=CD\left(cmt\right)\)
=> TỨ GIÁC ABCD LÀ HÌNH THOI
=> CÁC ĐƯỜNG CHÉO CẮT NHAU TẠI TRUNG ĐIỂM CỦA NÓ
=> \(OA=OC;OB=OD\)
mượn hình của Lê Trí Tiên làm tiếp câu (d)
vì M là trung điểm AD và O là trung điểm của AC => ON là đường trung bình tam giác ACD
=> ON //DC (1)
chứng minh tương tự ta có: OM là đường trung bình tam giác ACB
=> OM // AB mà AB // CD => OM // DC (2)
từ (1) (2) => M,O,N thằng hàng (đpcm)

Bạn tự vẽ hình nhé
a, Xét \(\Delta ABC\)và \(\Delta CDA\), ta có
\(\widehat{DAC}=\widehat{ACB}\left(gt\right)\)
AC: cạnh chung
\(\widehat{BAC}=\widehat{DCA}\left(gt\right)\)
do đó: \(\Delta ABC=\Delta CDA\left(g.c.g\right)\)
=>AD=BC(2 cạnh tương ứng)
=>AB=DC(2 cạnh tương ứng)
b, Ta có: BC=AD(CMT)
=>\(\frac{1}{2}BC=\frac{1}{2}AD\)=>MC=AN
Xét \(\Delta MAC\)và \(\Delta NCA\), ta có:
MC=AN(CMT)
\(\widehat{NAC}=\widehat{MCA}\) (2 góc so le trong)
AC:cạnh chung
do đó: \(\Delta MAC=\Delta NCA\left(c.g.c\right)\)
=>AM=CN(2 cạnh tương ứng)
c, Xét \(\Delta OAD\)và \(\Delta OCB\), ta có:
\(\widehat{DAO}=\widehat{BCO}\)(2 góc so le trong)
BC=AD(CMT)
\(\widehat{OBC}=\widehat{ADO}\)(2 góc so le trong)
do đó \(\Delta AOD=\Delta COB\left(g.c.g\right)\)
=> OA=OC(2 cạnh tương ứng)
=>OB=OD(2 cạnh tương ứng)
d,Sử dụng tiên đề Ơ-Clit...Bạn suy nghĩ đi mk chưa có cách giải chi tiết
Chúc bạn học tốt

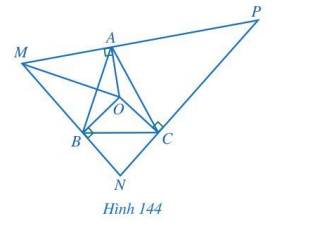
a) O là giao điểm của ba đường trung trực của tam giác ABC nên O cách đều ba đỉnh của tam giác đó hay OA = OB = OC.
Xét hai tam giác vuông OAM và OBM có:
OA = OB;
OM chung.
Vậy \(\Delta OAM = \Delta OBM\)(cạnh huyền – cạnh góc vuông).
Suy ra: \(\widehat {OMA} = \widehat {BMO}\) ( 2 góc tương ứng).
Vậy MO là tia phân giác của góc BMA hay MO là tia phân giác của góc NMP (ba điểm M, A, P thẳng hàng và ba điểm M, B, N thẳng hàng).
b) MO là tia phân giác của góc NMP.
Tương tự ta có:
NO là tia phân giác của góc MNP.
PO là tia phân giác của góc MPN.
Vậy O là giao điểm của ba đường phân giác MO, NO, PO của tam giác MNP.