Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2:
a: \(\sin\alpha=\sqrt{1-\left(\dfrac{2}{5}\right)^2}=\dfrac{\sqrt{21}}{5}\)
\(\tan\alpha=\dfrac{\sqrt{21}}{5}:\dfrac{2}{5}=\dfrac{\sqrt{21}}{2}\)
\(\cot\alpha=\dfrac{2}{\sqrt{21}}=\dfrac{2\sqrt{21}}{21}\)
b: Đặt \(\cos\alpha=a;\sin\alpha=b\)
Theo đề, ta có: a-b=1/5
=>a=b+1/5
Ta có: \(a^2+b^2=1\)
\(\Leftrightarrow b^2+\dfrac{2}{5}b+\dfrac{1}{25}+b^2-1=0\)
\(\Leftrightarrow2b^2+\dfrac{2}{5}b-\dfrac{24}{25}=0\)
\(\Leftrightarrow10b^2+2b-24=0\)
=>b=4/5
=>a=3/5
\(\cot\alpha=\dfrac{a}{b}=\dfrac{3}{4}\)

bài 1: ta có : \(cos^220+cos^240+cos^250+cos^270\)
\(=cos^220+cos^270+cos^240+cos^250\)
\(=cos^220+cos^2\left(90-20\right)+cos^240+cos^2\left(90-40\right)\)
\(=cos^220+sin^220+cos^240+sin^240=1+1=2\)
bài 2: a) ta có : \(cot^2\alpha-cos^2\alpha=cos^2\alpha\left(\dfrac{1}{sin^2\alpha}-1\right)=cos^2\alpha.\left(\dfrac{1-sin^2\alpha}{sin^2\alpha}\right)\)
\(=cos^2\alpha.\left(\dfrac{cos^2\alpha}{sin^2\alpha}\right)=cos^2\alpha.cot^2\alpha\left(đpcm\right)\)
b) ta có : \(sin^2\alpha+cos^2\alpha=1\Leftrightarrow sin^2\alpha=1-cos^2\alpha\)
\(\Leftrightarrow sin^2\alpha=\left(1-cos\alpha\right)\left(1+cos\alpha\right)\Leftrightarrow\dfrac{1+cos\alpha}{sin\alpha}=\dfrac{sin\alpha}{1-cos\alpha}\left(đpcm\right)\)

\(sin\alpha^2+cos\alpha^2=1\Rightarrow sin\alpha^2=1-cos\alpha^2=1-\dfrac{1}{25}=\dfrac{24}{25}\Rightarrow sin\alpha=\dfrac{2\sqrt{6}}{5}\)
\(\Rightarrow cot\alpha=\dfrac{cos\alpha}{sin\alpha}=\dfrac{1}{5}:\dfrac{2\sqrt{6}}{5}=\dfrac{1}{2\sqrt{6}}=\dfrac{\sqrt{6}}{24}\)
\(\sin^2\alpha+\cos^2\alpha=1\)
\(\Leftrightarrow\sin^2\alpha=1-\dfrac{1}{25}=\dfrac{24}{25}\)
hay \(\sin\alpha=\dfrac{2\sqrt{6}}{5}\)
\(\tan\alpha=\dfrac{\sin\alpha}{\cos\alpha}=\dfrac{2\sqrt{6}}{5}:\dfrac{1}{5}=2\sqrt{6}\)
\(\cot\alpha=\dfrac{1}{2\sqrt{6}}=\dfrac{\sqrt{6}}{12}\)

\(A=\left(sin^2a+cos^2a\right)\left(sin^4a-sin^2acos^2a+cos^4a\right)+3sin^2acos^2a\)
A = \(sin^4+2sin^2acos^2a+cos^4a=\left(sin^2a+cos^2a\right)^2=1\)

VT `=1+tan^2 α`
`=1+ (sin^2α)/(cos^2α)`
`= (cos^2α+sin^2α)/(cos^2α)`
`= 1/(cos^2α)`
a, \(1+tan^2a=\dfrac{1}{\cos^2a}\)
ĐT \(\Leftrightarrow\cos^2a\left(1+\tan^2a\right)=1\)
\(\Leftrightarrow\cos^2a+\cos^2a.\tan^2a=1\)
\(\Leftrightarrow\cos^2a.\dfrac{\sin^2a}{\cos^2a}+\cos^2a=\sin^2a+\cos^2a=1\) ( ĐT đã có )
=> ĐPCM
Vậy ...
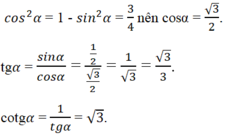
\(1+cot^2a=\dfrac{1}{sin^2a}\)
\(\Leftrightarrow\dfrac{1}{sin^2a}=1+\dfrac{\left(a^2-b^2\right)^2}{4a^2b^2}=\dfrac{4a^2b^2+a^4-2a^2b^2+b^4}{4a^2b^2}\)
\(\Leftrightarrow sin^2a=\dfrac{4a^2b^2}{a^4+2a^2b^2+b^4}=\left(\dfrac{2ab}{\left(a^2+b^2\right)}\right)^2\)
=>\(cos^2a=\dfrac{a^4+2a^2b^2+b^4-4a^2b^2}{\left(a^2+b^2\right)^2}\)
\(\Leftrightarrow cos^2a=\dfrac{\left(a^2-b^2\right)^2}{\left(a^2+b^2\right)^2}\)
hay \(cosa=\dfrac{\left(a^2-b^2\right)}{a^2+b^2}\)