H
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
26 tháng 3 2022
\(\dfrac{3sin\alpha-4cos\alpha}{2sin\alpha+3cos\alpha}=\dfrac{\dfrac{3sin\alpha}{cos\alpha}-\dfrac{4cos\alpha}{cos\alpha}}{\dfrac{2sin\alpha}{cos\alpha}+\dfrac{3cos\alpha}{cos\alpha}}=\dfrac{3tan\alpha-4}{2tan\alpha+3}\)
Biết tanα=\(-\dfrac{1}{4}\) nên ta có:
\(\dfrac{3\cdot\dfrac{-1}{4}-4}{2\cdot\dfrac{-1}{4}+3}=\dfrac{-\dfrac{3}{4}-4}{-\dfrac{1}{2}+3}=\dfrac{-19}{10}\)
CM
15 tháng 6 2018
Chọn A.
Áp dụng công thức biến đổi tổng thành tích và công thức nhân đôi; ta có
HT
21 tháng 7 2019
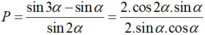
a/ \(VT=\frac{\sin^4x+2\sin x.\cos x-\left(1-\sin^2x\right)^2}{\frac{\sin2x}{\cos2x}-1}\)
\(=\frac{\sin^4x+2\sin x.\cos x-1+2\sin^2x-\sin^4x}{\frac{\sin2x-\cos2x}{\cos2x}}\) \(=\frac{1-2\sin^2x-\sin2x}{\frac{\cos2x-\sin2x}{\cos2x}}=\frac{\cos2x-\sin2x}{\frac{\cos2x-\sin2x}{\cos2x}}=\cos2x=VP\)
RH
18 tháng 2 2022
b)\(P=cos2a-cos(\dfrac{\pi}{3}-a) \\=2cos^2a-1-cos\dfrac{\pi}{3}cosa-sin\dfrac{\pi}{3}sina \\=2.(\dfrac{-2}{5})^2-1-\dfrac{1}{2}.\dfrac{-2}{5}-\dfrac{\sqrt3}{2}.\dfrac{-\sqrt{21}}{5} \\=\dfrac{-24+15\sqrt7}{50}\)
DT
18 tháng 2 2022
a, Vì : \(\pi< a< \dfrac{3\pi}{2}\) nên \(cos\alpha< 0\) mà \(cos^2\alpha=1-sin^2\alpha=1-\dfrac{4}{25}=\dfrac{21}{25},\)
do đó : \(cos\alpha=-\dfrac{\sqrt{21}}{5}\)
từ đó suy ra : \(tan\alpha=\dfrac{2}{\sqrt{21}},cot\alpha=\dfrac{\sqrt{21}}{2}\)