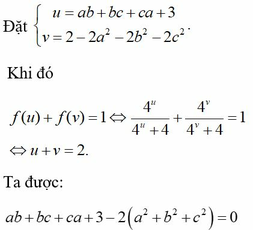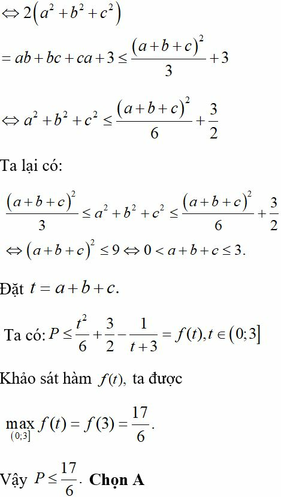Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
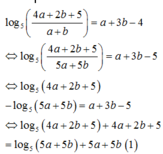
Xét hàm số
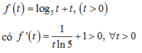
Hàm số f t đồng biến trên 0 ; + ∞
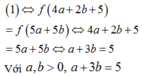
ta có:
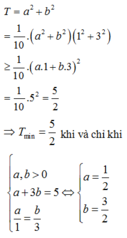
Chọn: D

Đáp án B
Ta có: log 5 4 a + 2 b + 5 a + b = a + 3 b − 4
⇔ log 5 4 a + 2 b + 5 + 4 a + 2 b + 5 = log 5 5 a + 5 b + 5 a + 5 b
Xét hàm số f t = log 5 t + t t > 0 ⇒ f t đồng biến trên 0 ; + ∞
Do đó f 4 a + 2 b + 5 = f 5 a + 5 b ⇔ 4 a + 2 b + 5 = 5 a + 5 b
⇔ a + 3 b = 5 ⇒ T = 5 − 3 b 2 + b 2 = 10 b 2 − 30 b + 25 = 10 b − 3 2 2 + 5 2 ≥ 5 2

15.
Ta có \(a+b+c+ab+bc+ac=6\)
Mà \(ab+bc+ac\le\left(a+b+c\right)^2\)
=> \(\left(a+b+c\right)^2+\left(a+b+c\right)-6\ge0\)
=> \(a+b+c\ge3\)
\(A=\frac{a^4}{ab}+\frac{b^4}{bc}+\frac{c^4}{ac}\ge\frac{\left(a^2+b^2+c^2\right)^2}{ab+bc+ac}\ge a^2+b^2+c^2\ge\frac{1}{3}\left(a+b+c\right)^2\ge3\)(ĐPCM)
Bài 18, Đặt \(\left(a^2-bc;b^2-ca;c^2-ab\right)\rightarrow\left(x;y;z\right)\) thì bđt trở thành
\(x^3+y^3+z^3\ge3xyz\)
\(\Leftrightarrow x^3+y^3+z^3-3xyz\ge0\)
\(\Leftrightarrow\left(x+y+z\right)\left(x^2+y^2+z^2-xy-yz-zx\right)\ge0\)
\(\Leftrightarrow\frac{1}{2}\left(x+y+z\right)\left[\left(x-y\right)^2+\left(y-z\right)^2+\left(z-x\right)^2\right]\ge0\)
Vì \(\left(x-y\right)^2+\left(y-z\right)^2+\left(z-x\right)^2\ge0\)nên ta đi chứng minh \(x+y+z\ge0\)
Thật vậy \(x+y+z=a^2-bc+b^2-ca+c^2-ab\)
\(=\frac{1}{2}\left[\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\right]\ge0\)(đúng)
Tóm lại bđt được chứng minh
Dấu "=": tại a=b=c

Đặt 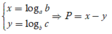 và giả thiết trở thành
và giả thiết trở thành
![]()
Suy ra ![]()
![]()
Phương trình có nghiệm khi ![]()
Chọn D.

Q=20-/3-x/ lớn nhất khi /3-x/ nhỏ nhất
nên /3-x/=0(vì /3-x/ luôn >=0 dấu)
3-x=0
x=3
D=4/\x-2\+2 lớn nhất khi và chỉ khi \x-2\+2 nhỏ nhất,khác 0 và lớn hơn=2(vì \x-2\ luôn EN)
nên \x-2\+2=2
\x-2\=0
x-2=0
x=2

a) Ta có:
\(M\left(x\right)=A\left(x\right)-2.B\left(x\right)+C\left(x\right)\)
\(=\left(2x^5-4x^3+x^2-2x+2\right)-2.\left(x^5-2x^4+x^2-5x+3\right)+\left(x^4+3x^3+3x^2-8x+4\frac{3}{16}\right)\)
\(=2x^5-4x^3+x^2-2x+2-2x^5+4x^4-2x^2+10x-6+x^4+4x^3+3x^2-8x+\frac{67}{16}\)
\(=\left(2x^5-2x^5\right)+\left(4x^4+x^4\right)+\left(-4x^3+4x^3\right)+\left(x^2-2x^2+3x^2\right)+\left(-2x+10x-8x\right)+\left(2-6+\frac{67}{16}\right)\)
\(=0+5x^4+0+2x^2+0+\frac{3}{16}\)
\(=5x^4+2x^2+\frac{3}{16}\)
b) Thay \(x=-\sqrt{0,25}=-0,5\); ta có:
\(M\left(-0,5\right)=5.\left(-0,5\right)^4+2.\left(-0,5\right)^2+\frac{3}{16}\)
\(=5.0,0625+2.0,25+\frac{3}{16}\)
\(=\frac{5}{16}+\frac{8}{16}+\frac{3}{16}=\frac{16}{16}=1\)
c) Ta có:
\(x^4\ge0\) với mọi x
\(x^2\ge0\) với mọi x
\(\Rightarrow5x^4+2x^2+\frac{3}{16}>0\) với mọi x
Do đó không có x để M(x)=0