Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Từ điều kiện đề bài suy ra $zx+zy=xy$
Khi đó:
$x^2+y^2+z^2=(x+y)^2-2xy+z^2=(x+y)^2+z^2-2(zx+zy)=(x+y)^2+z^2-2z(x+y)=(x+y-z)^2$
$\Rightarrow \sqrt{x^2+y^2+z^2}=|x+y-z|$
Vì $x,y,z$ là các số hữu tỉ nên $\sqrt{x^2+y^2+z^2}=|x+y-z|$ là số hữu tỉ (đpcm)
P/s: Bạn chú ý lần sau gõ đề bằng công thức toán.

Nếu x; y; z là các số nguyên dương mà x y z = 1 => x = y = z = 1
=> bất đẳng thức luôn xảy ra dấu bằng
Sửa đề 1 chút cho z; y; x là các số dương
Ta có: \(\frac{x^2}{y+1}+\frac{y+1}{4}\ge2\sqrt{\frac{x^2}{y+1}.\frac{y+1}{4}}=x\)
=> \(\frac{x^2}{y+1}\ge x-\frac{y+1}{4}\)
Tương tự:
\(\frac{x^2}{y+1}+\frac{y^2}{z+1}+\frac{z^2}{z+1}\ge x+y+z-\frac{y+1}{4}-\frac{z+1}{4}-\frac{x+1}{4}\)
\(=\frac{3}{4}\left(x+y+z\right)-\frac{3}{4}\ge\frac{3}{4}.3\sqrt[3]{xyz}-\frac{3}{4}=\frac{3}{2}\)
Dấu "=" xảy ra <=> x = y = z = 1

Ta có: \(x+y=z\Rightarrow x=z-y\)
\(A=\sqrt{\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}}=\sqrt{\dfrac{x^2y^2+y^2z^2+x^2z^2}{x^2y^2z^2}}\)
\(=\sqrt{\dfrac{\left(z-y\right)^2y^2+y^2z^2+\left(z-y\right)^2z^2}{x^2y^2z^2}}\)
\(=\sqrt{\dfrac{y^4+y^2z^2-2y^3z+y^2z^2+z^4+y^2z^2-2yz^3}{x^2y^2z^2}}\)
\(=\sqrt{\dfrac{\left(y^4+2y^2z^2+z^4\right)-2yz\left(y^2+z^2\right)+y^2z^2}{x^2y^2z^2}}\)
\(=\sqrt{\dfrac{\left(y^2+z^2\right)^2-2yz\left(y^2+z^2\right)+y^2z^2}{x^2y^2z^2}}\)
\(=\sqrt{\dfrac{\left(y^2+z^2-yz\right)^2}{x^2y^2z^2}}=\left|\dfrac{y^2+z^2-yz}{xyz}\right|\)
Là một số hữu tỉ do x,y,z là số hữu tỉ

Đặt \(\hept{\begin{cases}x+z=a\\y+z=b\end{cases}}\)thì giả thiết trở thành ab=1.
tìm Min \(\frac{1}{\left(a-b\right)^2}+\frac{1}{a^2}+\frac{1}{b^2}\)
ta có: \(\frac{1}{\left(a-b\right)^2}+\frac{1}{a^2}+\frac{1}{b^2}=\frac{1}{a^2+b^2-2}+a^2+b^2=\frac{1}{a^2+b^2-2}+a^2+b^2-2+2\)
Áp dụng bất đẳng thức AM-GM:\(\frac{1}{a^2+b^2-2}+a^2+b^2-2\ge2\)
do đó \(VT\ge4\)
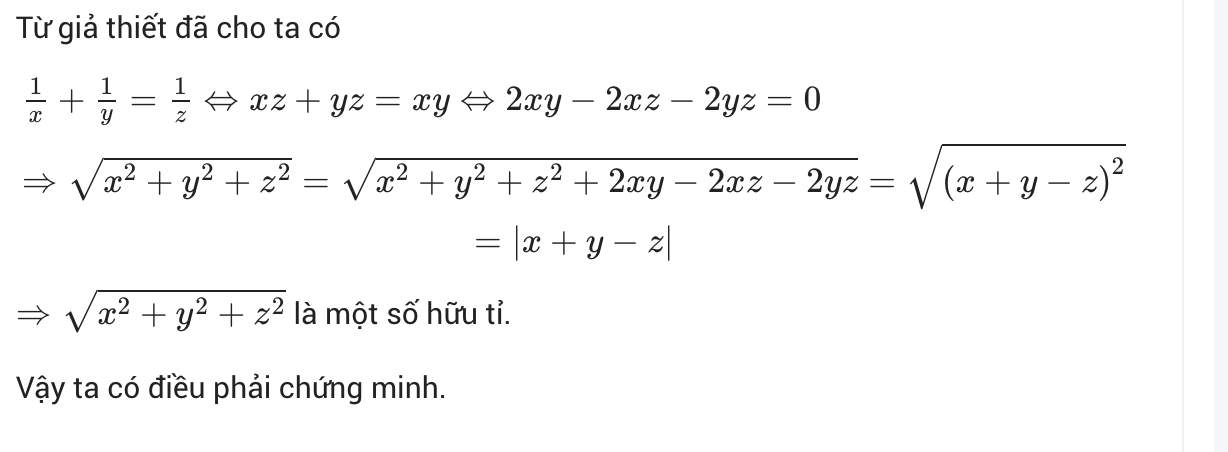
Ta có:
\(\sqrt{\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}}=\sqrt{\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}+0}=\sqrt{\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}+\dfrac{2\left(x+y+z\right)}{xyz}}\)
\(=\sqrt{\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}+\dfrac{2}{xy}+\dfrac{2}{yz}+\dfrac{2}{zx}}=\sqrt{\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)^2}\)
\(=\left|\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right|\) là số hữu tỉ