Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đồ thị hai hàm số \(y = 2mx - 2\) và \(y = 6x + 3\) song song với nhau khi:
\(\left\{ \begin{array}{l}2m = 6\\ - 2 \ne 3\end{array} \right. \Rightarrow 2m = 6 \Leftrightarrow m = 6:2 \Leftrightarrow m = 3\)
Vậy \(m = 3\) thì đồ thị hai hàm số \(y = 2mx - 2\) và \(y = 6x + 3\) song song với nhau.
Để hai hàm số song song:
=> 2m=6 <=> m=3

ĐKXĐ: m ≠ 0 và m ≠ 3/2
a) Đồ thị hai hàm số đã cho là hai đường thẳng song song khi:
m = 3 - 2m
m + 2m = 3
3m = 3
m = 1 (nhận)
Vậy m = 1 thì đồ thị hai hàm số đã cho là hai đường thẳng song song
b) Đồ thị hai hàm số đã cho là hai đường thẳng cắt nhau khi
m ≠ 3 - 2m
m + 2m ≠ 3
3m ≠ 3
m ≠ 1
Vậy m ≠ 0; m ≠ 1 và m ≠ 3/2 thì đồ thị hai hàm số đã cho là hai đường thẳng cắt nhau

Đồ thị hai hàm số \(y = kx - 1\) và \(y = 4x + 1\) cắt nhau khi: \(k \ne 4\).
Vậy để đồ thị hai hàm số \(y = kx - 1\) và \(y = 4x + 1\) cắt nhau thì \(k \ne 4\).

- Vẽ đồ thị hàm số \(y = x + 3\)
Cho \(x = 0 \Rightarrow y = 3\) ta được điểm \(A\left( {0;3} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{{ - 3}}{1} = - 3\) ta được điểm \(B\left( { - 3;0} \right)\) trên \(Ox\).
Đồ thị hàm số \(y = x + 3\) là đường thẳng đi qua hai điểm \(A\) và \(B\).
- Vẽ đồ thị hàm số \(y = - x + 3\)
Cho \(x = 0 \Rightarrow y = 3\) ta được điểm \(A\left( {0;3} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{{ - 3}}{{ - 1}} = 3\) ta được điểm \(C\left( {3;0} \right)\) trên \(Ox\).
Đồ thị hàm số \(y = - x + 3\) là đường thẳng đi qua hai điểm \(A\) và \(C\).
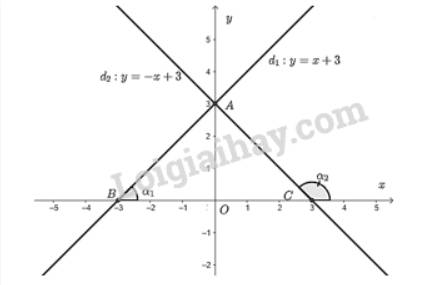
Từ đồ thị ta thấy giao điểm của hai đường thẳng là \(A\left( {0;3} \right)\).
Đường thẳng \({d_1}\) cắt trục \(Ox\) tại \(B\left( { - 3;0} \right)\).
Đường thẳng \({d_2}\) cắt trục \(Oy\) tại \(C\left( {3;0} \right)\).

Lời giải:
Vì đt $y=ax+b$ song song với $y=2x+2019$ nên $a=2$
$y=ax+b$ cắt trục tung tại điểm có tung độ $2020$, nghĩa là $(0,2020)\in (y=ax+b)$
$\Leftrightarrow 2020=a.0+b$
$\Rightarrow b=2020$
Vậy $a=2; b=2020$

a) Để đường thẳng \(y = 2mx - 5\) và đường thẳng \(y = 2x + 1\) song song với nhau thì \(\left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right. \Rightarrow \left\{ \begin{array}{l}2m = 2\\ - 5 \ne 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = 2:2\\ - 5 \ne 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = 1\\ - 5 \ne 1\end{array} \right.\left( {tm} \right)\)
Vậy \(m = 1\) thì hai đường thẳng \(y = 2mx - 5\) và \(y = 2x + 1\) song song với nhau.
b) Để đường thẳng \(y = 2mx - 5\) và đường thẳng \(y = 2x + 1\) cắt nhau thì \(a \ne a' \Rightarrow 2m \ne 2 \Leftrightarrow m \ne 2:2 \Leftrightarrow m \ne 1\).

Đồ thị hai hàm số \(y = 3nx + 4\) và \(y = 6x + 4\) trùng nhau khi:
\(\left\{ \begin{array}{l}3n = 6\\4 = 4\end{array} \right. \Rightarrow 3n = 6 \Leftrightarrow n = 6:3 \Leftrightarrow n = 2\)
Vậy \(n = 2\) thì đồ thị hai hàm số \(y = 3nx + 4\) và \(y = 6x + 4\) trùng nhau.

a: Gọi hàm số cần tìm có dạng là y=ax+b(a<>0)
Vì đồ thị của hàm số y=ax+b song song với đường thẳng y=5x+1 nên \(\left\{{}\begin{matrix}a=5\\b\ne1\end{matrix}\right.\)
Vậy: y=5x+b
Thay x=2 và y=-3 vào y=5x+b, ta được:
\(b+5\cdot2=-3\)
=>b+10=-3
=>b=-13
Vậy: y=5x-13
b: Thay y=5 vào y=2x-1, ta được:
2x-1=5
=>2x=6
=>x=3
Thay x=3 và y=5 vào y=ax+b, ta được:
\(a\cdot3+b=5\)
=>3a+b=5(1)
Thay x=2 và y=-3 vào y=ax+b, ta được:
2*a+b=-3
=>2a+b=-3(2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}3a+b=5\\2a+b=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3a+b-2a-b=5-\left(-3\right)\\2a+b=-3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=8\\b=-3-2a=-3-16=-19\end{matrix}\right.\)
vậy: y=8x-19
Đáp án đúng là D
- Đồ thị hàm số \(y = \dfrac{1}{3}x + 2\) là đường thẳng có hệ số góc là \(a = \dfrac{1}{3}\).
- Đồ thị hàm số \(y = - \dfrac{1}{3}x + 2\) là đường thẳng có hệ số góc là \(a = - \dfrac{1}{3}\).
- Đồ thị hàm số \(y = - 3x + 2\) là đường thẳng có hệ số góc là \(a = - 3\).
Vì cả ba đường thẳng đều có hệ số góc khác nhau nên chúng cắt nhau.
- Đồ thị hàm số \(y = \dfrac{1}{3}x + 2\) cắt trục tung tại điểm \(A\left( {0;2} \right)\).
- Đồ thị hàm số \(y = - \dfrac{1}{3}x + 2\) cắt trục tung tại điểm \(A\left( {0;2} \right)\)
- Đồ thị hàm số \(y = - 3x + 2\) cắt trục tung tại điểm \(A\left( {0;2} \right)\)
Do đó điểm \(A\left( {0;2} \right)\) là giao điểm của ba đồ thị hàm số.
Vậy đồ thị của các hàm số trên là các đường thẳng cắt nhau tại một điểm.