Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(P\left(x\right)+Q\left(x\right)-R\left(x\right)=2x^3+6x^2-5x+x^3-4x^3+3-5x^2+3x^3-x+4\)
\(=\left(2x^3+x^3-4x^3+3x^3\right)+\left(6x^2-5x^2\right)-\left(5x+x\right)+\left(3+4\right)\)
\(=2x^3+x^2-6x+7\)
Vậy \(P\left(x\right)+Q\left(x\right)-R\left(x\right)=2x^3+x^2-6x+7\)

\(P\left(x\right)=4x^4+2x^2-8x+\dfrac{1}{2}\)
\(Q\left(x\right)=-x^4-5x^2-8x-\dfrac{3}{4}\)
a: \(R\left(x\right)=P\left(x\right)-Q\left(x\right)=3x^4+7x^2+\dfrac{5}{4}\)
b: \(R\left(x\right)=3x^4+7x^2+\dfrac{5}{4}\ge\dfrac{5}{4}\forall x\)
nên R(X) không có nghiệm

\(P\left(x\right)=2x^2+3\)
\(Q\left(x\right)=-x^3+2x^2-x+2\)
\(Px-Qx=x^3+x+1\)
Px - Qx - Rx = 0 => Rx = -(x^3 + x +1)
Q(2) = -2^3 + 2.2^2 - 2 + 2 = 0 => x = 2 là nghiệm của Qx
P(2) = 2.2^2 + 3 = 11 khác 0 => x = 2 không phải là nghiệm của Px
-thaytoan.edu.vn-
a)P(x) = 4x2 + x3 - 2x + 3 - x - x3 + 3x - 2x2
= (4x2 - 2x2) + (x3 - x3) + (-2x - x + 3x) + 3
= 2x2 + 3
=> 2x2 + 3
Q(x) = 3x2 - 3x + 2 - x3 + 2x - x2
= (3x2 - x2) + (-3x + 2x) - x3 + 2
= 2x2 - x - x3 + 2
=> x3 - 2x2 - x + 2
c) Ta có:
P(2) = 2x2 + 3
= 2.22 + 3
= 11 (vô lý)
Q(2) = x3 - 2x2 - x + 2
= 23 - 2.22 - 2 + 2
= 0 (thỏa mãn)
Vậy x = 2 là nghiệm của Q(x) nhưng không phải là nghiệm của P(x)

a) Vì P(x) + Q(x) = x5 – 2x2 + 1 nên
Q(x) = x5 – 2x2 + 1 – P(x)
b) Vì P(x) – R(x) = x3 nên
R(x) = P(x) – x3

a ) Q ( x ) = [ P ( x ) + Q ( x ) ] - P ( x ) = ( x5 - 2x2 + 1 ) - ( x4 - 3x2+\(\frac{1}{2}\)- x ) = x5 - 2x2 + 1 - x4 + 3x2 - \(\frac{1}{2}\)+ x
= x5 - x4 - ( 2x2 - 3x2 ) + x + \(\frac{1}{2}\)
= x5 - x4 + x2 + x + \(\frac{1}{2}\)

Ta có: P(x) = x4 - 3x2 + \(\frac{1}{2}\) – x.
a) Vì P(x) + Q(x) = x5 – 2x2 + 1 nên
Q(x) = x5 – 2x2 + 1 - P(x)
Q(x) = x5 – 2x2 + 1 - x4 + 3x2 - \(\frac{1}{2}\) + x
Q(x) = x5 - x4 + x2 + x + \(\frac{1}{2}\)
b) Vì P(x) - R(x) = x3 nên
R(x) = x4 - 3x2 + \(\frac{1}{2}\) – x - x3
hay R(x) = x4 - x3 - 3x2 – x + \(\frac{1}{2}\)

a) \(P\left(x\right)=4x^2+x^3-2x+3-x-x^3+3x-2x^2\)
\(\Rightarrow P\left(x\right)=2x^2+3\)
\(Q\left(x\right)=3x^2-3x+2-x^3+2x-x^2\)
\(\Rightarrow Q\left(x\right)=-x^3+2x^2-x+2\)
b) \(P\left(x\right)-Q\left(x\right)-R\left(x\right)=0\Rightarrow P\left(x\right)-Q\left(x\right)=P\left(x\right)\)
\(R\left(x\right)=2x^2+3-\left(-x^3+2x^2-x+2\right)=2x^2+3+x^3-2x^2+x-2=x^3+x+1\)
c) Thay x = 2 vào đa thức Q ( x) ta được :
\(\left(-2\right)^3+2\left(2\right)^2-2+2=-8+2.4-2+2=-8+8-2+2=0\)
Vậy x = 2 là nghiệm của đa thức Q (x )
Thay x = 2 vào đa thức P(x) ta được:
\(2.2^2+3=2.4+3=8.3=16\)
Vậy x = 2 là nghiệm của đa thức P (x )
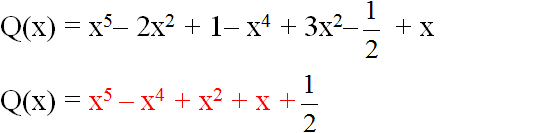
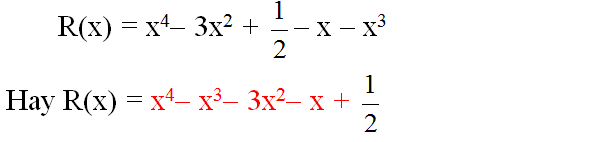
a,P (x)+Q (x)+Q (x)=(3x-2x2-2+6x3)+(3x2-x-2x3+4)+(1+4x3-2x)
=3x-2x2-2+6x3+3x2-x-2x3+4+1+4x3-2x
=(3x-x-2x)+(-2x2+3x2+3x2)+(-2+4+1)+(6x3-2x3+4x3)
=4x2+3+8x3
b,P (x)-Q (x)-R (x)=(3x-2x2-2+6x3)-(3x2-x-2x3+4)-(1+4x3-2x)
=3x-2x2-2+6x3-3x2+x+2x3-4-1+4x3-2x
=(3x +x-2x)+(-2x2-3x2)+(-2-4-1)+(2x3+4x3)
=2x-5x2-7 +6x3