Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(dkxd\Leftrightarrow\hept{\begin{cases}x\ge0\\\sqrt{x}-2\ne0\end{cases}\Rightarrow\hept{\begin{cases}x\ge0\\x\ne4\end{cases}}}\)
\(A=\left(\frac{\sqrt{x}}{x-4}-\frac{2}{\sqrt{x}-2}+\frac{1}{\sqrt{x}+2}\right):\frac{1}{\sqrt{x}+2}.\)
\(=\left(\frac{\sqrt{x}}{x-4}-\frac{2\left(\sqrt{x}+2\right)}{x-4}+\frac{\sqrt{x}-2}{x-4}\right):\frac{1}{\sqrt{x}+2}\)
\(=\frac{\sqrt{x}-2\sqrt{x}-4+\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}.\frac{\sqrt{x}+2}{1}\)
\(=\frac{-6\left(\sqrt{x}+2\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}=-\frac{6}{\sqrt{x}-2}\)
\(A=\)\(\left(\frac{\sqrt{x}}{x-4}+\frac{2}{2-\sqrt{x}}+\frac{1}{\sqrt{x}+2}\right)\)\(:\frac{1}{\sqrt{x}+2}\)
a,ĐKXĐ:\(\hept{\begin{cases}x\ge0\\2-\sqrt{x}\\x-4\ne0\end{cases}\ne0}\)\(\Rightarrow\)\(\hept{\begin{cases}x\ge0\\x\ne4\end{cases}}\)
\(A=\)\(\left(\frac{\sqrt{x}}{x-4}+\frac{2}{2-\sqrt{x}}+\frac{1}{\sqrt{x}+2}\right)\)\(:\frac{1}{\sqrt{x}+2}\)
\(A=\)\(\left(\frac{\sqrt{x}}{x-4}-\frac{2}{\sqrt{x}-2}+\frac{1}{\sqrt{x}+2}\right)\)\(.\left(\sqrt{x}+2\right)\)
\(A=\)\(\left(\frac{\sqrt{x}-2\left(\sqrt{x}+2\right)+\sqrt{x}-2}{x-4}\right)\)\(.\left(\sqrt{x}+2\right)\)
\(A=\)\(\left(\frac{\sqrt{x}-2\sqrt{x}-4+\sqrt{x}-2}{x-4}\right)\)\(.\left(\sqrt{x}+2\right)\)
\(A=\)\(\left(\frac{-6}{x-4}\right)\)\(.\left(\sqrt{x}+2\right)\)
\(A=\)\(\frac{-6}{\sqrt{x}-2}\)
b,\(x=9-4\sqrt{5}\)\(\Rightarrow\)\(A=\)\(\frac{-6}{\sqrt{9-4\sqrt{5}}-2}\)\(=\frac{-6}{\sqrt{5-2.2\sqrt{5}+4}-2}\)
\(A=\)\(\frac{-6}{\sqrt{\left(\sqrt{5}-2\right)^2}-2}\)\(=\frac{-6}{\sqrt{5}-2-2}\)\(=\frac{-6}{\sqrt{5}-4}\)
c,\(A>-1\)\(\Rightarrow\)\(\frac{-6}{\sqrt{x}-2}\)\(>-1\)\(\Rightarrow\)\(\frac{-6}{\sqrt{x}-2}+1>0\)
\(\Leftrightarrow\)\(\frac{-6+\sqrt{x}-2}{\sqrt{x}-2}>0\)
\(\Leftrightarrow\)\(\frac{\sqrt{x}-8}{\sqrt{x}-2}>0\)

i don't now
mong thông cảm !
...........................
Bạn đã trả lời một câu xàm lồn trên diễn đàn nên bị trừ điểm hỏi đáp còn 0

Thuy Duong Nguyen đánh đề cẩn thận hơn bạn nhé
Lời giải :
a) ĐKXĐ : \(x\ne1\)
\(A=\frac{15\sqrt{x}-11}{x+2\sqrt{x}-3}+\frac{3\sqrt{x}-2}{1-\sqrt{x}}-\frac{2\sqrt{x}+3}{\sqrt{x}+3}\)
\(A=\frac{15\sqrt{x}-11}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}+\frac{\left(\sqrt{x}+3\right)\left(2-3\sqrt{x}\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}-\frac{\left(2\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}\)
\(A=\frac{15\sqrt{x}-11-3x+6-7\sqrt{x}-2x-\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}\)
\(A=\frac{-5x+7\sqrt{x}-2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}\)
\(A=\frac{\left(\sqrt{x}-1\right)\left(-5\sqrt{x}+2\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}\)
\(A=\frac{2-5\sqrt{x}}{\sqrt{x}+3}\)
b) \(x=3-2\sqrt{2}=2-2\sqrt{2}+1=\left(\sqrt{2}-1\right)^2\)
\(\Leftrightarrow\sqrt{x}=\sqrt{2}-1\)
Khi đó \(A=\frac{2-5\left(\sqrt{2}-1\right)}{\sqrt{2}-1+3}\)
\(A=\frac{2-5\sqrt{2}+5}{\sqrt{2}+2}=\frac{7-5\sqrt{2}}{\sqrt{2}+2}\)
c) \(A=\frac{1}{2}\)
\(\Leftrightarrow\frac{2-5\sqrt{x}}{\sqrt{x}+3}=\frac{1}{2}\)
\(\Leftrightarrow2\left(2-5\sqrt{x}\right)=\sqrt{x}+3\)
\(\Leftrightarrow4-10\sqrt{x}-\sqrt{x}-3=0\)
\(\Leftrightarrow1-11\sqrt{x}=0\)
\(\Leftrightarrow11\sqrt{x}=1\)
\(\Leftrightarrow\sqrt{x}=\frac{1}{11}\)
\(\Leftrightarrow x=\frac{1}{121}\)( thỏa )
d) A nguyên \(\Leftrightarrow2-5\sqrt{x}⋮\sqrt{x}+3\)
\(\Leftrightarrow-5\left(\sqrt{x}+3\right)+17⋮\sqrt{x}+3\)
Vì \(-5\left(\sqrt{x}+3\right)⋮\sqrt{x}+3\)
\(\Rightarrow17⋮\sqrt{x}+3\)
\(\Rightarrow\sqrt{x}+3\inƯ\left(17\right)=\left\{17\right\}\)( vì \(\sqrt{x}+3\ge3\))
\(\Leftrightarrow\sqrt{x}=14\)
\(\Leftrightarrow x=196\)( thỏa )
Vậy....
\(a,ĐKXĐ:\orbr{\begin{cases}x+2\sqrt{x}+3\ne0\\\sqrt{x}+3\ne0\end{cases}}\)
\(\Leftrightarrow\orbr{ }\sqrt{x}\ne-3\)
Rút gọn: p/s: sau phân số thứ 2 ở mẫu ko có x à? Bạn chép đề sai?

Mn ơi giúp mình với. Please!!!!!!!!!!!!!!!!!!!!!!!!!!

a) \(ĐKXĐ:\hept{\begin{cases}x\ge0\\x\ne25\end{cases}}\)
\(A=\frac{x+3\sqrt{x}}{x-25}+\frac{1}{\sqrt{x}+5}\)
\(=\frac{x+3\sqrt{x}+\sqrt{x}-5}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}\)
\(=\frac{x+4\sqrt{x}-5}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}\)
\(=\frac{\sqrt{x}-1}{\sqrt{x}-5}\)
\(\Rightarrow P=\frac{\sqrt{x}-1}{\sqrt{x}-5}:\frac{\sqrt{x}+2}{\sqrt{x}-5}=\frac{\sqrt{x}-1}{\sqrt{x}+2}\)
b) Để P nguyên
\(\Leftrightarrow\sqrt{x}-1⋮\sqrt{x}+2\)
\(\Leftrightarrow3⋮\sqrt{x}+2\)
\(\Leftrightarrow\sqrt{x}+2\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{-3;-1;-5;1\right\}\)
Mà \(\sqrt{x}\ge0,\forall x\)
\(\Leftrightarrow\sqrt{x}=1\)
\(\Leftrightarrow x=1\)
Vậy để P nguyên \(\Leftrightarrow x=1\)
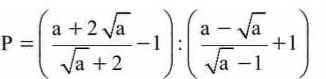 Bài 4. Cho biểu thức: P = ((a + 2sqrt(a))/(sqrt(a) + 2) - 1) / ((a - sqrt(a))/(sqrt(a) - 1) + 1)
Bài 4. Cho biểu thức: P = ((a + 2sqrt(a))/(sqrt(a) + 2) - 1) / ((a - sqrt(a))/(sqrt(a) - 1) + 1)