Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) sin a=0,8
Ta có: \(\sin^2a+\cos^2a=1\)
\(\Rightarrow\cos^2a=1-\sin^2a=1-0,8^2=0,36\)
\(\Rightarrow\orbr{\begin{cases}\cos a=0,6\\\cos a=-0,6\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}\tan a=\frac{4}{3}\\\tan a=\frac{-4}{3}\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}\cot a=\frac{3}{4}\\\cot a=\frac{-3}{4}\end{cases}}\)
\(\sin a=0,8\)
\(\sin^2a=1-\sin^2a=1\)
\(\cos^2a=1-\sin^2a=1-0,8^2=0,36\)
\(\Rightarrow\hept{\begin{cases}\cos a=0,6\\\cos a=-0,6\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}\tan a=\frac{4}{3}\\\tan a=\frac{-4}{3}\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}\cot a=\frac{3}{4}\\\cot a=\frac{-3}{4}\end{cases}}\)
Code : Breacker

a. Ta thấy \(\left(a\sqrt{5}\right)^2=\left(a\sqrt{3}\right)^2+\left(a\sqrt{2}\right)^2\Rightarrow AB^2=BC^2+AC^2\)
\(\Rightarrow\Delta ABC\)vuông tại C
b. \(\sin B=\frac{AC}{AB}=\frac{\sqrt{2}}{\sqrt{5}}=\frac{\sqrt{10}}{5};\cos B=\frac{CB}{AB}=\frac{\sqrt{3}}{\sqrt{5}}=\frac{\sqrt{15}}{5}\)
\(\tan B=\frac{AC}{AB}=\frac{\sqrt{6}}{3};\cot B=\frac{\sqrt{6}}{2}\)
\(\sin A=\cos B=\frac{\sqrt{15}}{5};\cos A=\sin B=\frac{\sqrt{10}}{5}\)
\(\tan A=\cot B=\frac{\sqrt{6}}{2};\cot A=\tan B=\frac{\sqrt{6}}{3}\)


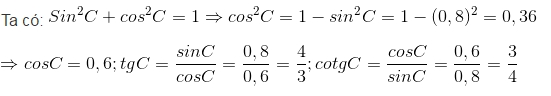
Làm tiêu biểu 1 bài thôi nhé. Các bài còn lại tương tự
a/ sin a = 0,8
Ta có: sin2 a + cos2 a = 1
=> cos2 a = 1 - sin2 a = 1 - 0,82 = 0,36
\(\Rightarrow\orbr{\begin{cases}cos\:a=0,6\\cos\:a=-0,6\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}tan\:a=\frac{4}{3}\\tan\:a=-\frac{4}{3}\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}cot\:a=\frac{3}{4}\\cot\:a=-\frac{3}{4}\end{cases}}\)