Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: AB//CD(vì ABCD là hình thang)
=>góc ABD=góc CDB
Xét tam giác ABD và tam giác CDB:
AB=DC(GT)
Góc ABD=Góc CDB(cmt)
DB là cạnh chung
Vậy tam giác ABD=tam giác CDB(c.g.c)
=>AD=BC(2 cạnh tương ứng); góc ADB=góc CBD( 2 góc tương ứng)
Ta có: góc ABD=góc CBD(cmt)
Mà 2 góc này nằm ở vị trí so le trong nên AD//BC(theo tiên đề Ơ-clit)(đpcm)

a/Ta có : M là Trung điểm của AD
N là trung diểm của BC
\(\Rightarrow\)MN là dường trung bình của hình thang
Theo định lí dường trung bình của hình thang( học tới đó thì cm minh ngay)
Thì MN=(AB+CD)/2
b/k có câu nào cho cm như vậy hết

a.
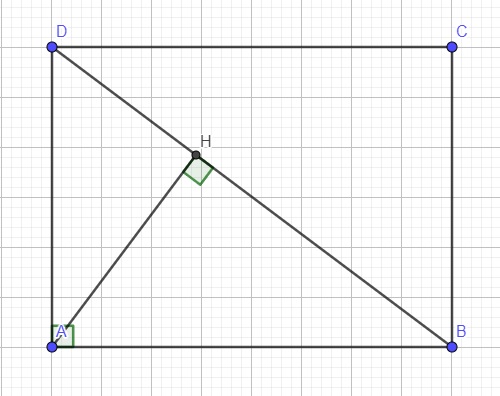
Do ABCD là hình chữ nhật \(\Rightarrow\widehat{HBA}=\widehat{CDB}\) (so le trong)
Xét hai tam giác HBA và CDB có:
\(\left\{{}\begin{matrix}\widehat{HBA}=\widehat{CDB}\left(cmt\right)\\\widehat{AHB}=\widehat{BCD}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta HBA\sim\Delta CDB\left(g.g\right)\)
b.
Xét hai tam giác AHD và BAD có:
\(\left\{{}\begin{matrix}\widehat{ADB}\text{ chung}\\\widehat{AHD}=\widehat{BAD}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta AHD\sim\Delta BAD\left(g.g\right)\)
\(\Rightarrow\dfrac{AD}{DB}=\dfrac{DH}{AD}\Rightarrow AD^2=DH.DB\)
c.
Áp dụng định lý Pitago cho tam giác vuông BAD:
\(DB=\sqrt{AD^2+AB^2}=\sqrt{BC^2+AB^2}=\sqrt{6^2+8^2}=10\left(cm\right)\)
Theo chứng minh câu b:
\(AD^2=DH.DB\Rightarrow DH=\dfrac{AD^2}{DB}=\dfrac{BC^2}{DB}=\dfrac{6^2}{10}=3,6\left(cm\right)\)
Áp dụng Pitago cho tam giác vuông AHD:
\(AH=\sqrt{AD^2-HD^2}=\sqrt{6^2-3,6^2}=4,8\left(cm\right)\)