TQ
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
EH
0
KH
1
4 tháng 1 2018
Ta có:AB=CD (gt)
AD=BC (gt)
=> Tứ giác ABCD là hình bình hành ( tứ giác có 2 cặp cạnh đối bằng nhau là hình bình hành)
=>AB//CD( tính chất hình bình hành) và AD//BC ( tính chất hình bình hành)
NN
0
NN
0
QT
2
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
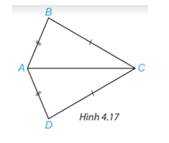
Xét tam giác \(\Delta ABC\) và \(\Delta ADC\) có:
\(\begin{array}{l}AB = AD(gt)\\BC = DC(gt)\\AC\,\,\,chung\end{array}\)
Suy ra \(\Delta ABC = \Delta ADC\)(c.c.c)
TG
18 tháng 9 2023
Xét 2 tam giác ABC và tam giác ADC ta có :
AB = AD
BC = DC
AC chung
=> ΔABC = ΔADC
23 tháng 2 2022
a: \(BC=\sqrt{34}\left(cm\right)\)
b: Xét ΔBCD có
CA là đường cao
CA là đường trung tuyến
Do đó:ΔCBD cân tại C
c: Xét ΔCKA vuông tại K và ΔCHA vuông tại H có
CA chung
\(\widehat{KCA}=\widehat{HCA}\)
Do đó: ΔCKA=ΔCHA
Suy ra: CK=CH
d: Xét ΔCBD có CK/CD=CH/CB
nên HK//BD