Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tham khảo lời giải sau:
Câu hỏi của Trần Thị Như Ý - Toán lớp 10 | Học trực tuyến

Lời giải:
a) Bạn tham khảo tại đây:
Câu hỏi của Trần Thị Như Ý - Toán lớp 10 | Học trực tuyến
b)
\(|\overrightarrow{OB}+\overrightarrow{AC}-\overrightarrow{OA}|=|\overrightarrow{OB}+\overrightarrow{AO}+\overrightarrow{OC}-\overrightarrow{OA}|\)
\(=|\overrightarrow{OB}+\overrightarrow{OC}-2\overrightarrow{OA}|\)
\(=|-\overrightarrow{OA}-2\overrightarrow{OA}|=3|\overrightarrow{OA}|=3a\)

Góc BOC = AOB - AOC = 100o - 60o = 40o
MOC = MOB = BOC : 2 = 40o : 2 = 20o
AOM = AOC + COM = 60o + 20o = 80o

\(\left|\overrightarrow{OA}\right|=\left|\overrightarrow{OB}\right|=\left|\overrightarrow{OC}\right|\Leftrightarrow OA=OB=OC\Leftrightarrow O\) là tâm đường tròn ngoại tiếp tam giác ABC (1)
\(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{0}\Leftrightarrow O\) là trọng tâm tam giác ABC (2)
(1); (2) \(\Rightarrow\) ABC là tam giác đều
\(\Rightarrow\widehat{AOB}=\widehat{BOC}=\widehat{COA}=120^0\)

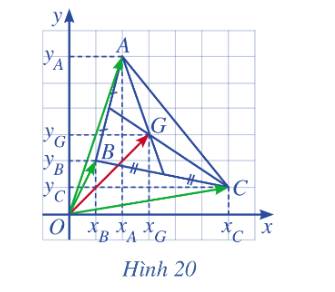
a) Ta có vectơ \(\overrightarrow {OG} \) theo ba vectơ \(\overrightarrow {OA} \) , \(\overrightarrow {OB} \)và \(\overrightarrow {OC} \) là: \(\overrightarrow {OG} = \frac{1}{3}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right)\)
b) Do tọa độ ba điểm A , B và C là: \(A\left( {{x_A},{y_A}} \right),B\left( {{x_B},{y_B}} \right),C\left( {{x_C},{y_C}} \right)\) nên ta có:\(\overrightarrow {OA} = \left( {{x_A},{y_A}} \right),\overrightarrow {OB} = \left( {{x_B},{y_B}} \right),\overrightarrow {OC} = \left( {{x_C},{y_C}} \right)\)
Vậy\(\overrightarrow {OG} = \frac{1}{3}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right) = \frac{1}{3}\left( {{x_A} + {x_B} + {x_C};{y_A} + {y_B} + {y_C}} \right) = \left( {\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3}} \right)\)
Tọa độ điểm G chính là tọa độ của vectơ \(\overrightarrow {OG} \) nên tọa độ G là \(G\left( {\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3}} \right)\)

a: \(\widehat{BOC}=\dfrac{1}{4}\cdot60^0=15^0\)
\(\widehat{AOB}=45^0\)
b: Vì \(\widehat{AOC}+\widehat{AOD}=90^0\)
nên hai góc này phụ nhau

Lời giải:
Giả sử độ dài 3 vecto đều bằng $a$.
$\cos \widehat{AOB}=\cos (\overrightarrow{OA}, \overrightarrow{OB})=\frac{\overrightarrow{OA}.\overrightarrow{OB}}{|\overrightarrow{OA}|.|\overrightarrow{OB}|}$
Trong đó:
$|\overrightarrow{OA}|.|\overrightarrow{OB}|=a.a=a^2$
$\overrightarrow{OA}.\overrightarrow{OB}=\frac{(\overrightarrow{OA}+\overrightarrow{OB})^2-(\overrightarrow{OA})^2-(\overrightarrow{OB})^2}{2}$
$=\frac{(-\overrightarrow{OC})^2-(\overrightarrow{OA})^2-(\overrightarrow{OB})^2}{2}$
$=\frac{a^2-a^2-a^2}{2}=\frac{-a^2}{2}$
Do đó: $\cos \widehat{AOB}=\frac{-a^2}{2a^2}=\frac{-1}{2}$
$\Rightarrow \widehat{AOB}=120^0$
Tương tự $\widehat{BOC}=\widehat{COA}=120^0$
đọc qua khó hiểu quá