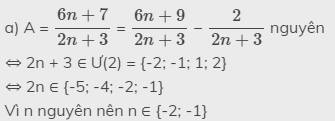Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) A = \(\dfrac{6n+7}{2n+3}\) = \(\dfrac{6n+9}{2n+3}\) − \(\dfrac{2}{2n+3}\) nguyên
⇔ 2n + 3 ∈ Ư(2) = {-2; -1; 1; 2}
⇔ 2n ∈ {-5; -4; -2; -1}
Vì n nguyên nên n ∈ {-2; -1}

Viết lại đề bài:
Tìm số nguyên x sao cho \(\frac{6}{x+1}.\frac{x-1}{3}\)là số nguyên
Giải:
\(\frac{6}{x+1}.\frac{x-1}{3}\text{}\)
\(=\frac{3.2}{x+1}.\frac{x-1}{3}\text{}\)
\(=\frac{3.2.\left(x-1\right)}{\left(x+1\right).3}\text{}\)
\(=\frac{3.2.\left(x-1\right)}{3.\left(x+1\right)}\)
\(=\frac{3.2.\left(x-1\right)}{3.\left(x+1\right)}\)
\(=\frac{2.\left(x-1\right)}{\left(x+1\right)}\)
\(=2.\frac{\left(x-1\right)}{\left(x+1\right)}\)
Bí....
Sorr nhak
Ta có:\(\frac{6x}{x+1}=\frac{6x+6-6}{x+1}=\frac{6\left(x+1\right)-6}{x+1}=6-\frac{6}{x+1}\)
Để\(\frac{6x}{x+1}\)là số nguyên \(\Leftrightarrow6⋮x+1\)
\(\Rightarrow x+1\inƯ\left(6\right)=\left\{-6;-3;-2;-1;1;2;3;6\right\}\)
\(\Rightarrow x=\left\{-7;-4;-3;-2;0;1;2;5\right\}\left(1\right)\)
Để\(\frac{x-1}{3}\)là số nguyên\(\Leftrightarrow\left(x-1\right)⋮3\)
\(\Rightarrow x-1=3k\Rightarrow x=3k+1\left(k\in Z\right)\left(2\right)\)
Từ (1) và (2)\(\Rightarrow x\in\left\{-2;1\right\}\)
Vậy \(x\in\left\{-2;1\right\}\)

x là số chắn
A=(-1)^n.3^n
A+3A=4A=1+(-1)^n.3^(n+1)
với x chẵn
A= [3^(x+1)+1]/4 vô nghiệm nguyên đề sai

Bài làm:
a) \(\left|\frac{1}{2}x-\frac{5}{2}\right|-1=-\frac{1}{2}\)
\(\Leftrightarrow\left|\frac{1}{2}x-\frac{5}{2}\right|=\frac{1}{2}\)
\(\Leftrightarrow\orbr{\begin{cases}\frac{1}{2}x-\frac{5}{2}=\frac{1}{2}\\\frac{1}{2}x-\frac{5}{2}=-\frac{1}{2}\end{cases}}\Leftrightarrow\orbr{\begin{cases}\frac{1}{2}x=3\\\frac{1}{2}x=2\end{cases}}\Rightarrow\orbr{\begin{cases}x=6\\x=4\end{cases}}\)
+ Nếu x = 6
\(\left|12-\frac{1}{3}y\right|=\frac{5}{6}\)
\(\Leftrightarrow\orbr{\begin{cases}12-\frac{1}{3}y=\frac{5}{6}\\12-\frac{1}{3}y=-\frac{5}{6}\end{cases}}\Leftrightarrow\orbr{\begin{cases}\frac{1}{3}y=\frac{67}{6}\\\frac{1}{3}y=\frac{77}{6}\end{cases}}\Rightarrow\orbr{\begin{cases}y=\frac{67}{2}\\y=\frac{77}{2}\end{cases}}\)
+ Nếu x = 4
\(\left|8-\frac{1}{3}y\right|=\frac{5}{6}\)
\(\Leftrightarrow\orbr{\begin{cases}8-\frac{1}{3}y=\frac{5}{6}\\8-\frac{1}{3}y=-\frac{5}{6}\end{cases}}\Leftrightarrow\orbr{\begin{cases}\frac{1}{3}y=\frac{43}{6}\\\frac{1}{3}y=\frac{53}{6}\end{cases}}\Rightarrow\orbr{\begin{cases}y=\frac{43}{2}\\y=\frac{53}{2}\end{cases}}\)
Vậy ta có 4 cặp số (x;y) thỏa mãn: \(\left(6;\frac{67}{2}\right);\left(6;\frac{77}{2}\right);\left(4;\frac{43}{2}\right);\left(4;\frac{53}{2}\right)\)
b) \(\frac{3}{2}x-\frac{1}{2}\left(x-\frac{2}{3}\right)=\frac{5}{3}\)
\(\Leftrightarrow\frac{3}{2}x-\frac{1}{2}x+\frac{1}{3}=\frac{5}{3}\)
\(\Leftrightarrow x=\frac{4}{3}\)
Thay vào ta được:
\(\frac{2.\frac{4}{3}+y}{\frac{4}{3}-2y}=\frac{5}{4}\)
\(\Leftrightarrow\frac{32}{3}+4y=\frac{20}{3}-10y\)
\(\Leftrightarrow14y=-4\)
\(\Rightarrow y=-\frac{2}{7}\)
Vậy ta có 1 cặp số (x;y) thỏa mãn: \(\left(\frac{4}{3};-\frac{2}{7}\right)\)