Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài này giải ra dài lắm;
Gợi ý : với câu a) cm 1<A<2
với câ u b) 0<B<1
với câu c) áp dụng bài toán của ông gao í; cách tỉnh tổng từ 1->100 trong sách GK 6 có nhé
Mong bạn giải ra

a) Xét:
\(a>b\)
\(\Rightarrow\dfrac{a}{b}>1\Rightarrow\dfrac{a+m}{b+m}>1\Rightarrow\dfrac{a}{b}>\dfrac{a+m}{a+m}\)
\(a< b\)
\(\Rightarrow\dfrac{a}{b}< 1\Rightarrow\dfrac{a+m}{b+m}< 1\Rightarrow\dfrac{a}{b}< \dfrac{a+m}{b+m}\)
\(a=b\)
\(\Rightarrow\dfrac{a}{b}=1\Rightarrow\dfrac{a+m}{b+m}=1\Rightarrow\dfrac{a}{b}=\dfrac{a+m}{b+m}=1\)
Mk chỉ áp dụng tính 1 câu,câu sau làm tương tự
b)
Ta có:
\(\dfrac{a}{b}< 1\Rightarrow\dfrac{a+m}{b+m}< 1\left(m\in N\right)\)
\(B=\dfrac{10^{1993}+1}{10^{1992}+1}< 1\)
\(B< \dfrac{10^{1993}+1+9}{10^{1992}+1+9}\Rightarrow B< \dfrac{10^{1993}+10}{10^{1992}+10}\Rightarrow B< \dfrac{10\left(10^{1992}+1\right)}{10\left(10^{1991}+1\right)}\Rightarrow B< \dfrac{10^{1992}+1}{10^{1991}+1}=A\)
\(B< A\)
@@ ~ học tốt ~

1)
a)
\(\dfrac{-21}{28}=\dfrac{\left(-21\right):7}{28:7}=\dfrac{-3}{4}\\ \dfrac{-39}{52}=\dfrac{\left(-39\right):13}{52:13}=\dfrac{-3}{4}\)
Vì \(\dfrac{-3}{4}=\dfrac{-3}{4}\) nên \(\dfrac{-21}{28}=\dfrac{-39}{52}\)
b)
\(\dfrac{-1717}{2323}=\dfrac{\left(-17\right)\cdot101}{23\cdot101}=\dfrac{-17}{23}\\ \dfrac{-171717}{232323}=\dfrac{\left(-17\right)\cdot10101}{23\cdot10101}=\dfrac{-17}{23}\)
Vì \(\dfrac{-17}{23}=\dfrac{-17}{23}\) nên \(\dfrac{-1717}{2323}=\dfrac{-171717}{232323}\)
2)
Theo tính chất cơ bản của phân số ta có: \(\dfrac{a}{b}=\dfrac{a\cdot m}{b\cdot m}\) mà \(m\ne n\)
nên không thể.
Trường hợp duy nhất là khi \(a=0\)
Khi đó: \(\dfrac{a}{b}=\dfrac{0}{b}=\dfrac{0\cdot m}{b\cdot n}=\dfrac{0}{b\cdot n}=0\)
3)
Gọi ƯCLN\(\left(12n+1,30n+2\right)\) là \(d\)
Ta có:
\(12n+1⋮d\\ \Rightarrow5\cdot\left(12n+1\right)⋮d\left(1\right)\\ \Leftrightarrow60n+5⋮d\\ 30n+2⋮d\\ \Rightarrow2\cdot\left(30n+2\right)⋮d\\ \Leftrightarrow60n+4⋮d\left(2\right)\)
Từ (1) và (2) ta có:
\(\left(60n+5\right)-\left(60n+4\right)⋮d\\ \Leftrightarrow1⋮d\\ \Rightarrow d=1\)
Vậy ƯCLN\(\left(12n+1,30n+2\right)=1\)
Mà hai số có ƯCLN = 1 thì hai số đó nguyên tố cùng nhau và không có ước chung nào khác
\(\Rightarrow\dfrac{12n+1}{30n+2}\)tối giản

Bài 2:
Tỉ số của số thứ nhất và số thứ hai là:
28/33:7/9=12/11
Số thứ nhất là 9:1x12=108
Số thứ hai là 108-9=99

\(a,\frac{20132013}{20142014}=\frac{2013.10001}{2014.10001}=\frac{2013}{2014}=1-\frac{1}{2014};\frac{131313}{141414}=\frac{13.10101}{14.10101}=\frac{13}{14}=1-\frac{1}{14}.\text{Vì: 14 bé hơn 2014 nên:}\frac{1}{14}>\frac{1}{2014}\Rightarrow\frac{20132013}{20142014}>\frac{131313}{141414}\)
\(C=2013^9+2013^9.2013=2013^9\left(2013+1\right)=2013^9.2014;D=2014^9.2014\text{ vì: 2013^9< 2014^9 nên: C bé thua D }\)
\(c,M=\frac{-7}{10^{2005}}+\frac{-15}{10^{2006}}=\frac{-7}{10^{2005}}+\frac{-7}{10^{2006}}+\frac{-8}{10^{2006}};N=\frac{-7}{10^{2005}}+\frac{-7}{10^{2006}}+\frac{-8}{10^{2005}}.Vì:10^{2006}>10^{2005}.Nên:\frac{-8}{10^{2006}}>\frac{-8}{10^{2005}}\Rightarrow M>N\)

Bài 2:
a: Để A là phân số thì x+6<>0
hay x<>-6
b: Để A là sốnguyen thì \(x+6-13⋮x+6\)
\(\Leftrightarrow x+6\in\left\{1;-1;13;-13\right\}\)
hay \(x\in\left\{-5;-7;7;-19\right\}\)
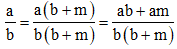
\(A=\dfrac{10}{a^m}+\dfrac{10}{a^n}\)
\(=\dfrac{10a^n+9a^m+a^m}{a^ma^n}\)
\(B=\dfrac{11}{a^m}+\dfrac{9}{a^n}\)
\(=\dfrac{10a^n+a^n+9a^m}{a^ma^n}\)
+ Nếu m > n thì am > an. \(\Rightarrow\) \(\dfrac{10a^n+9a^m+a^m}{a^ma^n}>\dfrac{10a^n+a^n+9a^m}{a^ma^n}\) hay A > B
+ Nếu m < n thì am < an. \(\Rightarrow\) \(\dfrac{10a^n+9a^m+a^m}{a^ma^n}< \dfrac{10a^n+a^n+9a^m}{a^ma^n}\) hay A < B
+ Nếu m = n thì am = an. \(\Rightarrow\) \(\dfrac{10a^n+9a^m+a^m}{a^ma^n}=\dfrac{10a^n+a^n+9a^m}{a^ma^n}\) hay A = B