Cho △ABC vuông tại A,kẻ đường cao AHa) Chứng minh △ABC đồng dạnh với △HAC và AB.AC=AH.BCb) Chứng minh A...

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

PN

Phạm Ngọc Minh Thư

11 tháng 3 2022

Cho △ABC vuông tại A,kẻ đường cao AH

a) Chứng minh △ABC đồng dạnh với △HAC và AB.AC=AH.BC

b) Chứng minh AC²=HC.BC

c) Chứng minh AH²=HB.HC

#Hỏi cộng đồng OLM #Toán lớp 8

2

KK

Kaito Kid

11 tháng 3 2022

KK

Kaito Kid

11 tháng 3 2022

undefined

Các câu hỏi dưới đây có thể giống với câu hỏi trên

PP

Phương Phương

27 tháng 4 2018

Cho ΔABC vuông tại A, AH là đường cao.

a) Cho AB = 6cm, BC=10cm. Tính AC ?

b) Chứng minh : AH.BC = AB.AC . Tính AH ?

c) Kẻ Hx // AB cắt AC tại K. Chứng minh : AH²= KA.KC

d) Chứng minh : ΔABC đồng dạng với ΔKAH

Giúp mình 2 câu cuối với ạ

#Hỏi cộng đồng OLM #Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

3 tháng 7 2022

a: AC=8cm

b: Xét ΔABC vuông tại A có AH là đường cao

nên \(AH\cdot BC=AB\cdot AC\)

hay AH=4,8(cm)

c: Xét ΔAHC vuông tại H có HK là đường cao

nên \(AH^2=AK\cdot AC\)

LX

Lệ Xuân

11 tháng 6 2020 - olm

Cho tam giác ABC vuông tại A, đường cao AH.

a. Chứng minh HA² = HB.HC

b. Tia phân giác góc HAC cắt HC tại P. Chứng minh BP²= BH.BC

c. Đường thẳng qua C và vuông góc với AC cắt tia AP tại K. Chứng minh KH=KC.

#Hỏi cộng đồng OLM #Toán lớp 8

0

SN

Sofia Nàng

18 tháng 3 2019 - olm

Cho tam giác ABC vuông tại A, AB < AC, AH là đường cao. a) Chứng minh tam giác HAC đồng dạng với tam giác ABC. b) Chứng minh HA2 = HB.HC c) Gọi D, E lần lượt là trung điểm của AB,AC. Chứng minh CH.CB = 4DE2 d) Gọi M là giao điểm của đường thẳng vuông góc với BC tại B và đường thẳng DE. Gọi N là giao điểm của AH và CM. Chứng minh N là trung điểm của...

#Hỏi cộng đồng OLM #Toán lớp 8

0

HT

Hoàng Thu Trang

12 tháng 2 2020 - olm

Cho tam giác ABC vuông tại A có đường cao AH. Chứng minh:

a. AH²= BH.CH

b. AH.BC= AB.AC

#Hỏi cộng đồng OLM #Toán lớp 8

2

I

Inequalities

12 tháng 2 2020

Áp dụng các hệ thức lượng trong tam giác vuông ,ta được:

\(AH^2=BH.CH\)

\(AH.BC=AB.AC\)

𝓛𝓪𝔃𝔂𝓑𝓪𝓬𝓸𝓷 ✨✨🥓🥓

12 tháng 2 2020

Lớp 8 chưa học lượng giác mà??

a) Xét tam giác AHC vuông tại H và tam giác AHB vuông tại H

Áp dụng định lý Pytago cho cả 2 tam giác:

Tam giác AHC: AH^2= AC^2 - CH^2 (1)

TAM GIÁC AHB: AH^2 =AB^2 - BH^2 (2)

(1) (2) Suy ra 2AH^2 = AB^2 + AC^2 - CH^2 - BH^2

2AH^2 = BC^2 - CH^2 - BH^2

2AH^2 = (BH+CH)^2 - CH^2 - BH^2

2AH^2 = 2BH.CH

AH^2 = BH.CH

b) Xét tam giác AHB và tam giác CAB:

H^ = A^ = 90 độ

B^ chung

2 tam giác AHB và tam giác CAB đồng dạng trường hợp (g-g)

Suy ra AH/CA = HB/AB= AB/BC

Vậy AH.BC = AB.AC

LX

Lệ Xuân

11 tháng 6 2020 - olm

Cho tam giác ABC vuông tại A, đường cao AH.

a. Chứng minh HA² = HB.HC

b. Tia phân giác góc HAC cắt HC tại P. Chứng minh BP²= BH.BC

c. Đường thẳng qua C và vuông góc với AC cắt tia AP tại K. Chứng minh KH=KC.

Giúp mình câu c với ạ mình cảm ơn

#Hỏi cộng đồng OLM #Toán lớp 8

0

ND

Nhã Doanh

26 tháng 1 2018

Cho tam giác ABC vuông tại A, đường cao AH.

a. chứng minh AB² = BH . BC và AC² = CH.BC

b. Chứng minh BC² = AB² +AC²

c. chứng minh: AH² = BH.CH

d. chứng minh: AH.BC=AB.AC

e. chứng minh: 1/AH² = 1/AB²+ 1/AC²

#Hỏi cộng đồng OLM #Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

16 tháng 6 2022

a: Xét ΔABH vuông tại H và ΔCBA vuông tại A có

góc B chung

Do đó: ΔABH\(\sim\)ΔCBA

Suy ra: BA/BC=BH/BA

hay \(BA^2=BH\cdot BC\)

Xét ΔACH vuông tại H và ΔBCA vuông tại A có

góc C chung

Do đo: ΔACH\(\sim\)ΔBCA
Suy ra: CA/CB=CH/CA

hay \(CA^2=CH\cdot CB\)

b: \(BC^2=AB^2+AC^2\)

c: Xét ΔAHB vuông tại H và ΔCHA vuông tại H có

\(\widehat{HAB}=\widehat{HCA}\)

Do đó: ΔAHB\(\sim\)ΔCHA

Suy ra: HA/HC=HB/HA

hay \(HA^2=HB\cdot HC\)

TN

Thien Nguyen

28 tháng 5 2020

Bài 2: Cho tam giác ABC vuông tại A có AB = 15cm, AC = 20cm, AH là đường cao. a) Chứng minh tam giác HBA đồng dạng với tam giác HAC b) Chứng minh AB2 = BH.BC; AC2 = HC.BC, HA2 = HB.HC c) Tính độ dài các cạnh BC, HB, AH d) Đường phân giác của góc ABC cắt AC tại D. Tính AD, DC e) Từ D kẻ đường vuông góc với BC tại H (H thuộc BC). Chứng minh CH.CB =...

#Hỏi cộng đồng OLM #Toán lớp 8

0

BN

Bảo Ngọc Phan Trần

25 tháng 2 2020

: Cho tam giác ABC vuông tại A, đường cao AH.

a. Chứng minh tam giác ABC đồng dạng tam giác HBA từ đó suy ra AB² = BC.BH

a. Chứng minh tam giác ABC đồng dạng với tam giác HAC từ đó suy ra AH² = HB.HC

b. Giả sử AB = 6, AC=8; Tính AH, HB

#Hỏi cộng đồng OLM #Toán lớp 8

0

TN

Thien Nguyen

31 tháng 5 2020

HELP ME!!!!! Cho tam giác ABC vuông tại A có AB = 15cm, AC = 20cm, AH là đường cao. a) Chứng minh tam giác HBA đồng dạng với tam giác HAC b) Chứng minh AB2 = BH.BC; AC2 = HC.BC, HA2 = HB.HC c) Tính độ dài các cạnh BC, HB, AH d) Đường phân giác của góc ABC cắt AC tại D. Tính AD, DC e) Từ D kẻ đường vuông góc với BC tại H (H thuộc BC). Chứng minh CH.CB = CD.CA ...

#Hỏi cộng đồng OLM #Toán lớp 8

2

TH

Trương Huy Hoàng

31 tháng 5 2020

Phần a là HBA ~ ABC chứ nhỉ?

a, Xét tam giác HBA và tam giác ABC có:

góc BHA = góc BAC = 90^o (ABC vg tại A và AH là đường cao)

góc B chung

\(\Rightarrow\) \(\Delta\)HBA ~ \(\Delta\)ABC (gg)

b, Vì \(\Delta\)HBA ~ \(\Delta\)ABC (cmt) (1)

Tương tự ta cx có: \(\Delta\)HAC ~ \(\Delta\)ABC (2)

Từ (1) và (2) \(\Rightarrow\) \(\Delta\)HBA ~ \(\Delta\)HAC

\(\Rightarrow\) \(\frac{AH}{CH}=\frac{BH}{AH}\) hay AH² = CH . BH (đpcm)

Vì \(\Delta\)HBA ~ \(\Delta\)ABC (cmt)

\(\Rightarrow\) \(\frac{AB}{BC}=\frac{BH}{AB}\) hay AB² = BC . BH (đpcm)

Vì \(\Delta\)HAC ~ \(\Delta\)ABC (cmt)

\(\Rightarrow\) \(\frac{AC}{BC}=\frac{HC}{AC}\) hay AC² = BC . HC (đpcm)

c, Xét tam giác ABC vg tại A có: BA\(\perp\)CA

\(\Rightarrow\) BC² = AB² + AC²(định lí Pytago)

BC² = 15² + 20²

BC² = 625

BC = \(\sqrt{625}\) = 25 (cm)

Vì \(\Delta\)HBA ~ \(\Delta\)ABC (cmt)

\(\Rightarrow\) \(\frac{AB}{BC}=\frac{BH}{AB}\)

hay \(\frac{15}{25}=\frac{BH}{15}\) \(\Rightarrow\) BH = \(\frac{15^2}{25}\) = 9 (cm)

Vì BH = 9 cm nên CH = 25 - 9 = 16 (cm)

Vì \(\Delta\)HBA ~ \(\Delta\)HAC (cmt)

\(\Rightarrow\) \(\frac{AH}{CH}=\frac{BH}{AH}\) hay \(\frac{AH}{16}=\frac{9}{AH}\)

\(\Rightarrow\) \(AH^2=16\cdot9=144\)

\(\Rightarrow\) \(AH=\sqrt{144}=12\) (cm)

d, Xét tam giác ABC có: BD là tia p/g của góc ABC (gt)

\(\Rightarrow\) \(\frac{AD}{AB}=\frac{CD}{BC}\) (t/c đường p/g của tam giác)

hay \(\frac{20-CD}{15}=\frac{CD}{25}\)

\(\Leftrightarrow\) \(\frac{5\left(20-CD\right)}{75}=\frac{3CD}{75}\)

\(\Rightarrow\) 5(20 - CD) = 3CD

\(\Leftrightarrow\) 100 - 5CD = 3CD

\(\Leftrightarrow\) 3CD + 5CD = 100

\(\Leftrightarrow\) 8CD = 100

\(\Leftrightarrow\) CD = 12,5 (cm)

\(\Rightarrow\) AD = 20 - 12,5 = 7,5 (cm)

e, Ko thể có 2 điểm H được nên mk gọi D vuông góc với BC tại M nha!

Xét tam giác CMD và tam giác CAB có:

góc CMD = góc CAB = 90^o (DM \(\perp\) BC và \(\Delta\)ABC vg tại A theo gt)

góc C chung

\(\Rightarrow\) \(\Delta\)CMD ~ \(\Delta\)CAB (gg)

\(\Rightarrow\) \(\frac{CM}{CA}=\frac{CD}{CB}\) hay CM . CB = CD . CA (đpcm)

Chúc bn học tốt!! (Dài quá :vvv)

NL

Nguyễn Lê Phước Thịnh

31 tháng 5 2020

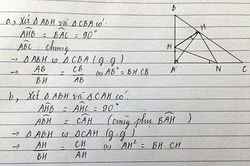
a) Xét ΔHBA và ΔABC có

\(\widehat{AHB}=\widehat{CAB}\left(=90^0\right)\)

\(\widehat{ABC}\) chung

Do đó: ΔHBA∼ΔABC(g-g)(1)

Xét ΔHAC và ΔABC có

\(\widehat{AHC}=\widehat{BAC}\left(=90^0\right)\)

\(\widehat{ACB}\) chung

Do đó: ΔHAC∼ΔABC(g-g)(2)

Từ (1) và (2) suy ra ΔHBA∼ΔHAC(đpcm)

b) Ta có: ΔHBA∼ΔABC(cmt)

⇒\(\frac{HB}{AB}=\frac{BA}{BC}=\frac{HA}{AC}=k_1\)(tỉ số đồng dạng)

hay \(AB^2=BC\cdot BH\)(đpcm)

Ta có: ΔHAC∼ΔABC(cmt)

⇒\(\frac{HA}{AB}=\frac{AC}{BC}=\frac{HC}{AC}=k_2\)(tỉ số đồng dạng)

hay \(AC^2=BC\cdot HC\)(đpcm)

Ta có: ΔHBA∼ΔHAC(cmt)

⇒\(\frac{HB}{HA}=\frac{HA}{HC}=\frac{BA}{AC}=k\)(tỉ số đồng dạng)

hay \(HA^2=HB\cdot HC\)(đpcm)

c) Áp dụng định lí pytago vào ΔABC vuông tại A, ta được:

\(BC^2=AB^2+AC^2\)

⇔\(BC^2=15^2+20^2=625\)

hay \(BC=\sqrt{625}=25cm\)

Ta có: \(AB^2=BC\cdot BH\)(cmt)

⇔\(15^2=25\cdot BH\)

⇔\(BH=\frac{15^2}{25}=\frac{225}{25}=9cm\)

Ta có: \(\frac{HA}{AB}=\frac{AC}{BC}=\frac{HC}{AC}\)(cmt)

⇔\(\frac{HA}{15}=\frac{20}{25}\)

⇔\(HA=\frac{15\cdot20}{25}=\frac{300}{25}=12cm\)

Vậy: BC=25cm; BH=9cm; HA=12cm

d) Xét ΔABC có BD là đường phân giác ứng với cạnh AC(gt)

nên \(\frac{AD}{AB}=\frac{CD}{CB}\)(tính chất đường phân giác của tam giác)

hay \(\frac{AD}{15}=\frac{CD}{25}\)

Ta có: AD+CD=AC(D nằm giữa A và C)

hay AD+CD=20cm

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\frac{AD}{15}=\frac{CD}{25}=\frac{AD+CD}{15+25}=\frac{20}{40}=\frac{1}{2}\)

Do đó:

\(\left\{{}\begin{matrix}\frac{AD}{15}=\frac{1}{2}\\\frac{CD}{25}=\frac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AD=\frac{15\cdot1}{2}=7,5cm\\CD=\frac{25\cdot1}{2}=12,5cm\end{matrix}\right.\)

Vậy: AD=7,5cm; CD=12,5cm

e) Đề sai rồi bạn