Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tam giác ABC = tam giác DEI
-> Các cạnh tương ứng của hai tam giác đều bằng nhau
mà AB = 5 (cm), AC = 6 (cm), EI = 8(cm)
-> Chu vi tam giác ABC = chu vi tam giác DEI = AB + AC + EI = 5 + 6 + 8 = 19 (cm)
Vậy chu vi hai hình tam giác đó đều bằng 19 cm.

\(\Delta ABC=\Delta DEI\)
\(\Rightarrow AB=DE=5\left(cm\right)\) ( 2 cạnh tương ứng )
\(\Rightarrow BC=EI=8\left(cm\right)\) ( 2 cạnh tương ứng )
\(\Rightarrow AC=DI=6\left(cm\right)\) ( 2 cạnh tương ứng )
Chu vi của \(\Delta ABC\) là:
\(AB+BC+CA=5+8+6=19\left(cm\right)\)
Chu vi của \(\Delta DEI\) là:
\(DE+EI+DI=5+8+6=19\left(cm\right)\)
Vậy...........

Vì tam giác ABC= tam giác DEI
=> AB= DE ( 2 cạnh tg ứng)
BC=EI ( 2 cạnh tg ứng)
AC= DI ( 2 cạnh tg ứng)
Mà AB= 5 => DE= 5
AC= 6 => DI =6
EI= 8 => BC= 8
Vậy chu vi tam giác ABC là : 5+6+8= 19
Mà tam giác DEI = tam giác ABC => chu vi cũng = 19

ΔABC=DEFΔABC=DEF
=> AB=DE=3cm; BC=EF=5cm; AC=DF=4cm.
Diện tích ΔABCΔABC=Diện tích ΔDEFΔDEF=3+5+4=12 (cm)
Đ/S:12
ai k mik 3 cái mik k lại 9 cái
#mai

ΔABC=ΔDEIΔABC=ΔDEI
⇒AB=DE=5(cm)⇒AB=DE=5(cm) ( 2 cạnh tương ứng )
⇒BC=EI=8(cm)⇒BC=EI=8(cm) ( 2 cạnh tương ứng )
⇒AC=DI=6(cm)⇒AC=DI=6(cm) ( 2 cạnh tương ứng )
Chu vi của ΔABCΔABC là:
AB+BC+CA=5+8+6=19(cm)AB+BC+CA=5+8+6=19(cm)
Chu vi của ΔDEIΔDEI là:
DE+EI+DI=5+8+6=19(cm)DE+EI+DI=5+8+6=19(cm)
Vậy........
ΔABC=ΔDEf
⇒AB=DE=5(cm) ( 2 cạnh tương ứng )
⇒BC=EI=8(cm) ( 2 cạnh tương ứng )
⇒AC=DI=6(cm) ( 2 cạnh tương ứng )
Chu vi của ΔABCΔABC là:
AB+BC+CA=5+8+6=19(cm)
Chu vi của ΔDEIΔDEI là:
DE+EI+DI=5+8+6=19(cm)
Vậy........

a ) vì cùng vuông góc với AC
b ) ta có HAC + HCA = 90 độ
ABC + HCA = 90 độ
nên HAC=ABC
ta có HAC + AHE=90 độ
mà HAC = ABC = 60 độ
nên AHE = 90-60 = 30 độ
BAH + HAC = 90 độ
BAH = 90 - 60 = 30 độ

A B E F D C
ta có : \(\Delta\)ABC = \(\Delta DEF\)
=> góc A = góc D
góc B = góc E
góc C = góc F
AB = DE = 4cm
BC = EF = 6cm
CA = FD = 5cm
chu vi của tam giác ABC là :
4 + 5 + 6 = 15 ( cm )
mà tam giác ABC = tam giác DEF
=> chu vi tam giác DEF = 15 cm

Vì \(\Delta ABC=\Delta DEF\)
nên AB = DE = 4cm;
BC = EF = 6cm;
AC = DF = 5cm
Khi đó: \(P_{\Delta ABC}=P_{\Delta DEF}=4+5+6=15\left(cm\right)\)
Vậy \(P_{\Delta ABC}=P_{\Delta DEF}=15cm.\)

Vì ΔABC=ΔDEI⇒EI=BC
⇒chu vi của ΔABC là: \(8+7+9=24\left(cm\right)\)
⇒chu vi của ΔBEI là: \(24\left(cm\right)\)

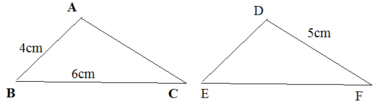
Vì ΔABC = ΔDEF nên suy ra:
AB = DE = 4cm
BC = EF = 6cm
DF = AC = 5cm
Chu vi tam giác ABC bằng:
AB + BC + CA = 4 + 6 + 5 = 15 (cm)
Chu vi tam giác DEF bằng:
DE + EF + DF = 4 + 6 + 5 = 15 (cm)
Ta có: ΔABC=ΔDEI(gt)
=> BC=EI=8cm(2 cạnh tương ứng)
Ta có: \(P_{DEI}=P_{ABC}=AB+AC+BC=5+6+8=19\left(cm\right)\)
(Với P là chu vi)