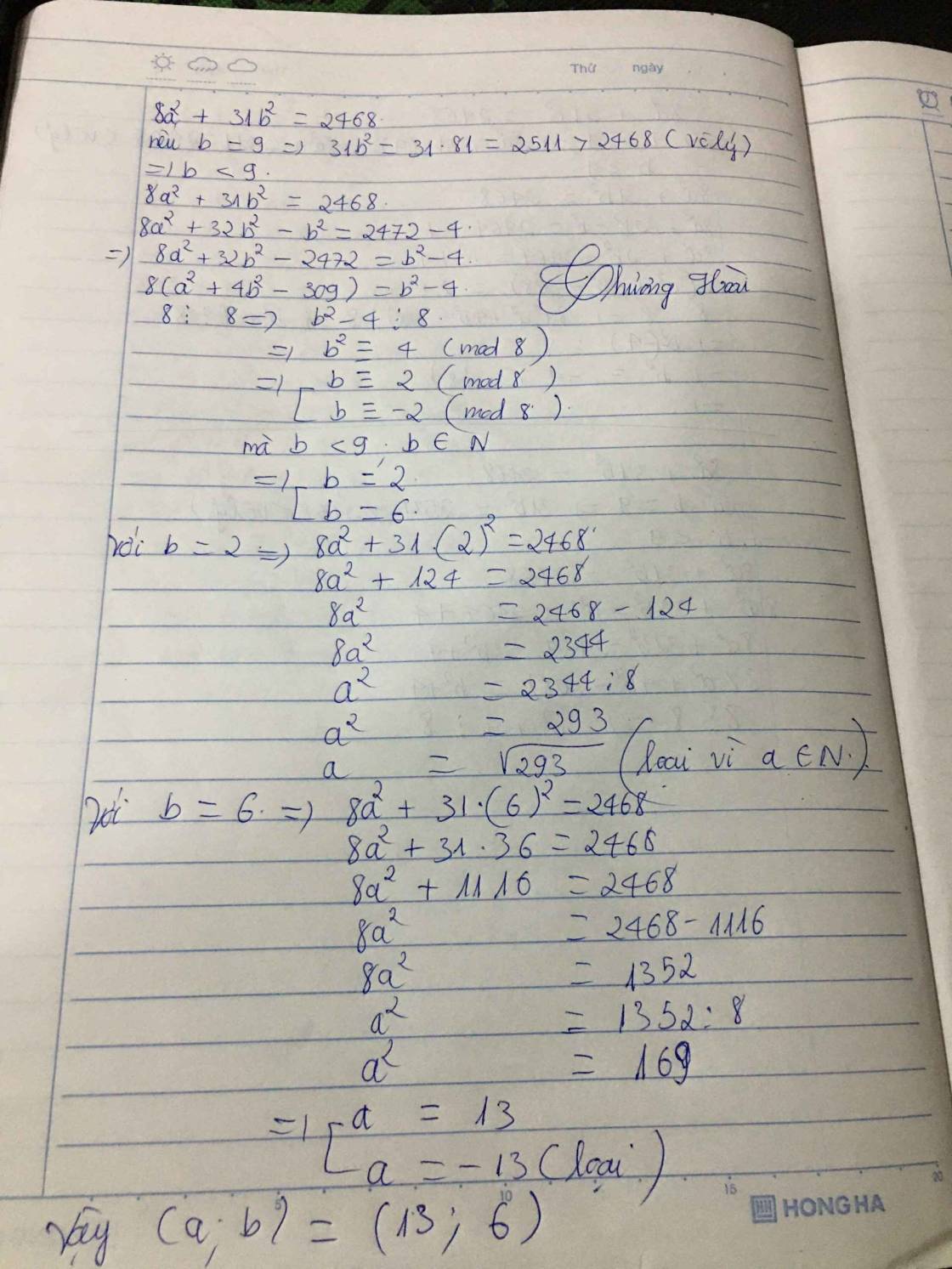Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Vì $a,b$ là số tự nhiên nên $2a+1,b-2$ là số nguyên
$(2a+1)(b-2)=12$ nên $2a+1$ là ước của $12$
Mà $2a+1$ là số tự nhiên lẻ nên $2a+1\in\left\{1;3\right\}$
Nếu $2a+1=1$ thì $b-2=12:1=12$
$\Rightarrow a=0; b=14$ (thỏa mãn)
Nếu $2a+1=3$ thì $b-2=12:3=4$
$\Rightarrow a=1; b=6$ (thỏa mãn)

a)vì n \(\varepsilon\)N* =>n>=1
mà c^n=1=>c=1
Vậy c=1
b)vì n>=1 mà c^n=0
=>c=0
Vậy c=0

Chào bạn!
Ta sẽ chứng minh bài toán này theo phương pháp phản chứng
Giả sử \(\left(a;c\right)=m\)\(V\text{ới}\)\(m\in N\)\(m\ne1\)
Khi đó \(\hept{\begin{cases}a=k_1m\\c=k_2m\end{cases}}\)
Thay vào \(ab+cd=p\)ta có : \(k_1mb+k_2md=p\Leftrightarrow m\left(k_1b+k_2d\right)=p\)
Khi đó p là hợp số ( Mâu thuẫn với đề bài)
Vậy \(\left(a;c\right)=1\)(đpcm)

=>2ab-3a+b-9=0
=>b(2a+1)-3a-4,5-*4,5=0
=>b(2a+1)-1,5(2a+1)=4,5
=>(2a+1)(b-1,5)=4,5
=>(2a+1)(2b-3)=9
=>\(\left(2a+1;2b-3\right)\in\left\{\left(1;9\right);\left(3;3\right);\left(9;1\right)\right\}\)
=>\(\left(a,b\right)\in\left\{\left(0;6\right);\left(1;3\right);\left(4;2\right)\right\}\)

Bạn dùng phương pháp chặn `b` rồi tìm `a` nhé.
`8a^2 + 31b^2 = 2468 <=> 31b^2 <= 2468 <=> b^2 < 81 -> b = 1 -> 8.`
Từ đây tìm `a` theo `b` và nhớ thử lại nhé.

=>3b(4a-3)+20a-15=2820
=>(4a-3)(3b+5)=2820
=>a chia 4 dư 1, b chia 3 dư 2
Do đó: \(\left(a,b\right)\in\varnothing\)

\(\frac{a}{5}-\frac{2}{b}=\frac{2}{15}\Leftrightarrow\frac{a}{5}-\frac{2}{15}=\frac{2}{b}\Leftrightarrow\frac{3a-2}{15}=\frac{2}{b}\Leftrightarrow\left(3a-2\right)b=30\)
Ta có bảng sau:
| 3a-2 | 1 | 2 | 3 | 5 | 6 | 10 | 15 | 30 |
| b | 30 | 15 | 10 | 6 | 5 | 3 | 2 | 1 |
| a | 1 | 4/3 | 5/3 | 7/3 | 8/3 | 4 | 17/3 | 32/3 |
Vì a;b là các số tự nhiên nên có 2 cặp số a;b thỏa mãn là ...

B=ax.by⇒B2=a2x.b2yB=ax.by⇒B2=a2x.b2y ; B3=a3x.a3yB3=a3x.a3y
⇒⇒ số ước số tự nhiên của B2B2 là (2x+1)(2y+1)(2x+1)(2y+1)
⇒(2x+1)(2y+1)=15⇒(2x+1)(2y+1)=15
⇒⇒{2x+1=32y+1=5{2x+1=32y+1=5 ⇒{x=1y=2⇒{x=1y=2 hoặc {2x+1=52y+1=3{2x+1=52y+1=3 ⇒{x=2y=1⇒{x=2y=1
⇒⇒ số ước của B3B3 là (3x+1)(3y+1)=4.7=28