Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
Ta có M nằm trên trục Oy nên tọa độ điểm M có dạng M(0; y)
Ba điểm A; B; M thẳng hàng khi ![]() cùng phương với
cùng phương với ![]()
Ta có ![]() . Do đó,
. Do đó, ![]() cùng phương với
cùng phương với
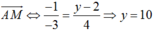
Vậy M(0; 10) .

Gọi \(M\left(0;m\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AM}=\left(-1;m+2\right)\\\overrightarrow{AB}=\left(-5;7\right)\end{matrix}\right.\)
3 điểm M;A;B thẳng hàng khi:
\(\dfrac{-1}{-5}=\dfrac{m+2}{7}\Rightarrow m=-\dfrac{3}{5}\)
\(\Rightarrow M\left(0;-\dfrac{3}{5}\right)\)

Chọn A.
Hai điểm A(1;2) và B(4;6) ⇒ AB = 5
Gọi M(0;m).
Vì diện tích tam giác MAB bằng 1
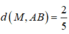
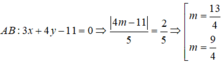

a: A(1;2); B(2;1)
=>\(\overrightarrow{AB}=\left(1;-1\right)\)
=>VTPT là (1;1)
Phương trình đường thẳng AB là:
1(x-1)+2(y-1)=0
=>x-1+2y-2=0
=>x+2y-3=0
b:
M(1;3); Δ: 3x+4y+10=0
Khoảng cách từ M đến Δ là:
\(d\left(M;\text{Δ}\right)=\dfrac{\left|1\cdot3+3\cdot4+10\right|}{\sqrt{3^2+4^2}}=\dfrac{\left|3+12+10\right|}{5}=5\)

a/ Để tứ giác ADCB là hbh
\(\Leftrightarrow\overrightarrow{AD}=\overrightarrow{BC}\Leftrightarrow\left(x_D-x_A;y_D-y_A\right)=\left(x_C-x_B;y_C-y_B\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_D-1=4+2\\y_D-2=4-6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_D=7\\y_D=0\end{matrix}\right.\Rightarrow D\left(7;0\right)\)
b/ Có phải đề bài là:
\(2\overrightarrow{EA}-4\overrightarrow{EB}+\overrightarrow{EC}=\overrightarrow{0}?\)
\(\Rightarrow2\left(x_A-x_E;y_A-y_E\right)-4\left(x_B-x_E;y_B-y_E\right)+\left(x_C-x_E;y_C-y_E\right)=0\)
\(\Leftrightarrow2\left(1-x_E;2-y_E\right)-4\left(-2-x_E;6-y_E\right)+\left(4-x_E;4-y_E\right)=0\)
\(\Rightarrow\left\{{}\begin{matrix}2-2x_E+8+4x_E+4-x_E=0\\4-2y_E-24+4y_E+4-y_E=0\end{matrix}\right.\)
Bạn tự giải nốt

Bài này có vài cách giải, do M thuộc Oy nên tọa độ đơn giản, dùng công thức khoảng cách là dễ nhất:
Gọi \(M\left(0;a\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AM}=\left(-1;a-2\right)\\\overrightarrow{MB}=\left(2;5-a\right)\end{matrix}\right.\)
\(\Rightarrow T=AM+BM=\sqrt{1^2+\left(a-2\right)^2}+\sqrt{2^2+\left(5-a\right)^2}\)
\(\Rightarrow T\ge\sqrt{\left(1+2\right)^2+\left(a-2+5-a\right)^2}=3\sqrt{2}\)
\(\Rightarrow T_{min}=3\sqrt{2}\) khi \(\frac{a-2}{1}=\frac{5-a}{2}\Rightarrow a=3\Rightarrow M\left(0;3\right)\)
Gọi \(M\left(0;y\right)\) thì ta có :
\(\overrightarrow{AB}=\left(-3;4\right)\) ; \(\overrightarrow{AM}=\left(-1;y-2\right)\)
Để A,B,M thẳng hàng thì \(\overrightarrow{AB}=k.\overrightarrow{AM}\) , tức là :
\(\begin{cases}k.\left(-1\right)=-3\\k.\left(y-2\right)=4\end{cases}\) \(\Rightarrow\begin{cases}k=3\\y=\frac{10}{3}\end{cases}\)
Vậy để A,B,M thẳng hàng thì \(M\left(0;\frac{10}{3}\right)\)