Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

* Cách 1 :
Ta có :
\(16A=\frac{4^{17}+16}{4^{17}+1}=\frac{4^{17}+1+15}{4^{17}+1}=\frac{4^{17}+1}{4^{17}+1}+\frac{15}{4^{17}+1}=1+\frac{15}{4^{17}+1}\)
\(16B=\frac{4^{14}+16}{4^{14}+1}=\frac{4^{14}+1+15}{4^{14}+1}=\frac{4^{14}+1}{4^{14}+1}+\frac{15}{4^{14}+1}=1+\frac{15}{4^{14}+1}\)
Vì \(\frac{15}{4^{17}+1}< \frac{15}{4^{14}+1}\) nên \(1+\frac{15}{4^{17}+1}< 1+\frac{15}{4^{14}+1}\)
\(\Rightarrow\)\(16A< 16B\) hay \(A< B\)
Vậy \(A< B\)
Chúc bạn học tốt ~
\(4^2.A=\frac{4^2\left(4^{15}+1\right)}{4^{17}+1}\); \(4^2.B=\frac{4^2\left(4^{12}+1\right)}{4^{14}+1}\)
=> \(4^2.A=\frac{4^{17}+4^2}{4^{17}+1}\);\(4^2.B=\frac{4^{14}+4^2}{4^{14}+1}\)
=> \(4^2.A=\frac{4^{17}+1+4^2-1}{4^{17}+1}\); \(4^2.B=\frac{4^{14}+1+4^2-1}{4^{14}+1}\)
=> \(4^2.A=\frac{4^{17}+1}{4^{17}+1}+\frac{4^2-1}{4^{17}+1}\); \(4^2.B=\frac{4^{14}+1}{4^{14}+1}+\frac{4^2-1}{4^{14}+1}\)
=> \(4^2.A=1+\frac{4^2-1}{4^{17}+1}\); \(4^2.B=1+\frac{4^2-1}{4^{14}+1}\)
Mà \(4^{17}>4^{14}\)
=> \(4^{17}+1>4^{14}+1\)
=> \(\frac{4^2-1}{4^{17}+1}< \frac{4^2-1}{4^{14}+1}\)
=> \(1+\frac{4^2-1}{4^{17}+1}< 1+\frac{4^2-1}{4^{14}+1}\)
=> \(4^2.A< 4^2.B\)
=> \(A< B\)

4 mũ 15+1/4 mũ 17 +1= 1/16+1
4 mũ 12+1/ 4 mũ 14+1= 1/16+1
suy ra 1/17=1/17
suy ra A=B
nhớ tích cho tớ nhé

Câu1:
a: \(=2008^2-\left(2008-2\right)\left(2008+2\right)\)
\(=2008^2-\left(2008^2-4\right)\)
=4
b: \(=\dfrac{23\cdot29\cdot10101}{23\cdot29\cdot10101}=1\)
c: \(=\dfrac{\left(2^{17}+5^{17}\right)\left(3^{14}-5^{12}\right)\cdot\left(16-16\right)}{15^2+5^3+67^7}\)
=0

a) \(\dfrac{-1}{-4}\)=\(\dfrac{1}{4}>0\)
\(\dfrac{3}{-4}< 0\)
\(\Rightarrow\dfrac{1}{4}>\dfrac{3}{-4}hay\dfrac{-1}{-4}>\dfrac{3}{-4}\)
b) Ta có:
\(\dfrac{15}{17}=1-\dfrac{2}{17}\\ \)
\(\dfrac{25}{27}=1-\dfrac{2}{27}\\ \\ \)
Mà \(\dfrac{2}{17}>\dfrac{2}{27}\left(17< 27\right)\)
\(\Rightarrow1-\dfrac{2}{17}< 1-\dfrac{2}{27}\)hay \(\dfrac{15}{17}< \dfrac{25}{27}\)

Ta có :
\(\dfrac{1}{11}>\dfrac{1}{20}\\ \dfrac{1}{12}>\dfrac{1}{20}\\ ..........\\ \dfrac{1}{20}=\dfrac{1}{20}\)
\(\Rightarrow\dfrac{1}{11}+\dfrac{1}{12}+\dfrac{1}{13}+...+\dfrac{1}{20}>\dfrac{1}{20}+\dfrac{1}{20}+...+\dfrac{1}{20}\\ \Rightarrow S>\dfrac{10}{20}\\ \Rightarrow S>\dfrac{1}{2}\)

Câu 2:
\(A=2014+\dfrac{2014}{1+2}+\dfrac{2014}{1+2+3}+...+\dfrac{2014}{1+2+3+...+2013}\)
\(=2014\left(1+\dfrac{1}{1+2}+\dfrac{1}{1+2+3}+...+\dfrac{1}{1+2+3+...+2013}\right)\)
\(=2014\left(1+\dfrac{1}{2\left(2+1\right)}.2+\dfrac{1}{3\left(3+1\right)}.2+...+\dfrac{1}{2013\left(2013+1\right)}.2\right)\)
\(=2014\left(\dfrac{2}{1.2}+\dfrac{2}{2.3}+\dfrac{2}{3.4}+...+\dfrac{2}{2013.2014}\right)\)
\(=4028\left(\dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{2013.2014}\right)\)
Bạn tự tính nốt nhé
1)
\(A=\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{2012^2}< \dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{2011\cdot2012}\left(1\right)\)\(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{2011\cdot2012}\\ =\dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2011}-\dfrac{1}{2012}\\ =\dfrac{1}{1}-\dfrac{1}{2012}< 1\left(2\right)\)
Từ (1) và (2) ta có: A < 1
2)
\(A=2014+\dfrac{2014}{1+2}+\dfrac{2014}{1+2+3}+...+\dfrac{2014}{1+2+3+...+2013}\\ =2014\cdot\left(\dfrac{1}{1}+\dfrac{1}{1+2}+\dfrac{1}{1+2+3}+...+\dfrac{1}{1+2+3+...+2013}\right)\\ =2014\cdot\left(\dfrac{1}{\left(1\cdot2\right):2}+\dfrac{1}{\left(2\cdot3\right):2}+\dfrac{1}{\left(3\cdot4\right):2}+...+\dfrac{1}{\left(2013\cdot2014\right):2}\right)\\ =2014\cdot\left(\dfrac{2}{1\cdot2}+\dfrac{2}{2\cdot3}+\dfrac{2}{3\cdot4}+...+\dfrac{2}{2013\cdot2014}\right)\\ =2014\cdot2\cdot\left(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{2013\cdot2014}\right)\\ =4028\cdot\left(\dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2013}-\dfrac{1}{2014}\right)\\ =4028\cdot\left(1-\dfrac{1}{2014}\right)\\ =4028\cdot\dfrac{2013}{2014}\\ =4026\)
3)
Để A là số nguyên thì \(6n+42⋮6n\Rightarrow42⋮6n\Rightarrow6n\inƯ\left(42\right)\)
\(Ư\left(42\right)=\left\{1;2;3;6;7;14;21;42\right\}\)
| 6n | 1 | 2 | 3 | 6 | 7 | 14 | 21 | 42 |
| n | \(\dfrac{1}{6}\) | \(\dfrac{1}{3}\) | \(\dfrac{1}{2}\) | 1 | \(\dfrac{7}{6}\) | \(\dfrac{7}{3}\) | \(\dfrac{7}{2}\) | 7 |
Vì n là số tự nhiên nên n = 1 hoặc n = 7
4)
\(A=\dfrac{17^{18}+1}{17^{19}+1}< \dfrac{17^{18}+1+16}{17^{19}+1+16}=\dfrac{17^{18}+17}{17^{19}+17}=\dfrac{17\cdot\left(17^{17}+1\right)}{17\cdot\left(17^{18}+1\right)}=\dfrac{17^{17}+1}{17^{18}+1}=B\)
Vậy A<B

c) E = \(\dfrac{4116-14}{10290-35}\) và K = \(\dfrac{2929-101}{2.1919+404}\)
E = \(\dfrac{4116-14}{10290-35}\)
E = \(\dfrac{14.\left(294-1\right)}{35.\left(294-1\right)}\)
E = \(\dfrac{14}{35}\)
K = \(\dfrac{2929-101}{2.1919+404}\)
K = \(\dfrac{101.\left(29-1\right)}{101.\left(38+4\right)}\)
K = \(\dfrac{29-1}{34+8}\)
K = \(\dfrac{28}{42}\) = \(\dfrac{2}{3}\)
Ta có : E = \(\dfrac{14}{35}\) và K = \(\dfrac{2}{3}\)
\(\dfrac{14}{35}\) = \(\dfrac{42}{105}\)
\(\dfrac{2}{3}\) = \(\dfrac{70}{105}\)
Vậy E < K
Các câu còn lại tương tự

a) \(\left(1-\dfrac{1}{3}\right)\left(1-\dfrac{1}{6}\right)\left(1-\dfrac{1}{10}\right)...\left(1-\dfrac{1}{780}\right)\)
\(=\dfrac{2}{3}.\dfrac{5}{6}.\dfrac{9}{10}.....\dfrac{779}{780}\)\(=\)
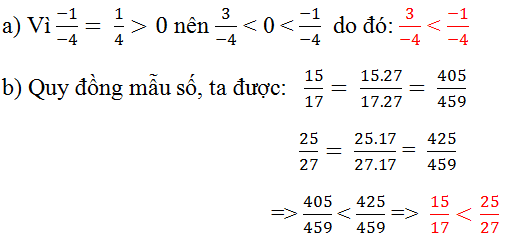
Ta có: \(16\cdot A=\dfrac{16\cdot\left(4^{15}+1\right)}{4^{17}+1}\)
\(\Leftrightarrow16\cdot A=\dfrac{4^{17}+16}{4^{17}+1}=1+\dfrac{15}{4^{17}+1}\)
Ta có: \(16\cdot B=\dfrac{16\cdot\left(4^{12}+1\right)}{4^{14}+1}\)
\(\Leftrightarrow16\cdot B=\dfrac{4^{14}+16}{4^{14}+1}=1+\dfrac{15}{4^{14}+1}\)
Ta có: \(4^{17}+1>4^{14}+1\)
\(\Leftrightarrow\dfrac{15}{4^{17}+1}< \dfrac{15}{4^{14}+1}\)
\(\Leftrightarrow\dfrac{15}{4^{17}+1}+1< \dfrac{15}{4^{14}+1}+1\)
\(\Leftrightarrow16A< 16B\)
hay A<B