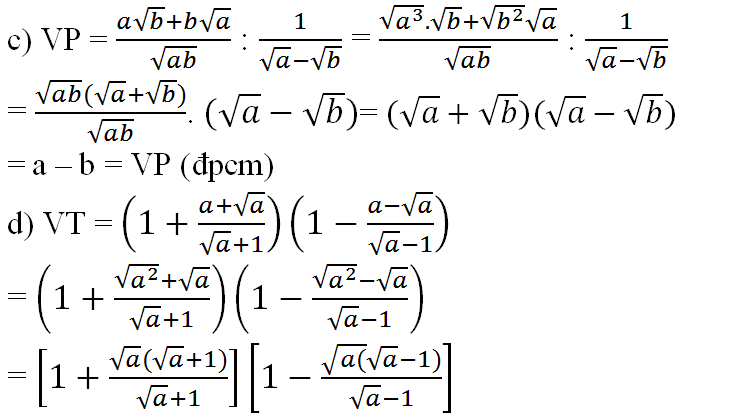Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt \(a^{\dfrac{1}{9}};b^{\dfrac{1}{9}};c^{\dfrac{1}{9}}\rightarrow x;y;z\)\(\left(x;y;z>0;xyz=1\right)\)
Ta có BĐT:\(\dfrac{1}{\sqrt{8x^9+1}}\ge\dfrac{1}{x^8+x^4+1}\)
\(\Leftrightarrow\dfrac{\dfrac{\left(x-1\right)^2x^4\left(x^{10}+2x^9+3x^8+4x^7+7x^6+10x^5+13x^4+8x^3+6x^2+4x+2\right)}{\left(x^2-x+1\right)^2\left(x^2+x+1\right)^2\left(2x^3+1\right)\left(x^4-x^2+1\right)^2\left(4x^6-2x^3+1\right)}}{\dfrac{1}{\sqrt{8x^9+1}}+\dfrac{1}{x^8+x^4+1}}\ge0\)
Tương tự cho 2 BĐT còn lại rồi cộng theo vế:
\(A\ge\dfrac{1}{x^8+x^4+1}+\dfrac{1}{y^8+y^4+1}+\dfrac{1}{z^8+z^4+1}\ge1\)
Dấu "=" khi \(x=y=z=a=b=c=1\)

Bài 1:
Áp dụng BĐT Bunhiacopxky:
\(M^2=(a\sqrt{9b(a+8b)}+b\sqrt{9a(b+8a)})^2\)
\(\leq (a^2+b^2)(9ab+72b^2+9ab+72a^2)\)
\(\Leftrightarrow M^2\leq (a^2+b^2)(72a^2+72b^2+18ab)\)
Áp dụng BĐT AM-GM: \(a^2+b^2\geq 2ab\Rightarrow 18ab\leq 9(a^2+b^2)\)
Do đó, \(M^2\leq (a^2+b^2)(72a^2+72b^2+9a^2+9b^2)=81(a^2+b^2)^2\)
\(\Leftrightarrow M\leq 9(a^2+b^2)\leq 144\)
Vậy \(M_{\max}=144\Leftrightarrow a=b=\sqrt{8}\)
Bài 6:
\(a+\frac{1}{a-1}=1+(a-1)+\frac{1}{a-1}\)
Vì \(a>1\rightarrow a-1>0\). Do đó áp dụng BĐT Am-Gm cho số dương\(a-1,\frac{1}{a-1}\) ta có:
\((a-1)+\frac{1}{a-1}\geq 2\sqrt{\frac{a-1}{a-1}}=2\)
\(\Rightarrow a+\frac{1}{a-1}=1+(a-1)+\frac{1}{a-1}\geq 3\) (đpcm)
Dấu bằng xảy ra khi \(a-1=1\Leftrightarrow a=2\)
Bài 3:
Xét \(\sqrt{a^2+1}\). Vì \(ab+bc+ac=1\) nên:
\(a^2+1=a^2+ab+bc+ac=(a+b)(a+c)\)
\(\Rightarrow \sqrt{a^2+1}=\sqrt{(a+b)(a+c)}\)
Áp dụng BĐT AM-GM có: \(\sqrt{(a+b)(a+c)}\leq \frac{a+b+a+c}{2}=\frac{2a+b+c}{2}\)
hay \(\sqrt{a^2+1}\leq \frac{2a+b+c}{2}\)
Hoàn toàn tương tự với các biểu thức còn lại và cộng theo vế:
\(\sqrt{a^2+1}+\sqrt{b^2+1}+\sqrt{c^2+1}\leq \frac{2a+b+c}{2}+\frac{2b+a+c}{2}+\frac{2c+a+b}{2}=2(a+b+c)\)
Ta có đpcm. Dấu bằng xảy ra khi \(a=b=c=\frac{1}{\sqrt{3}}\)
Bài 4:
Ta có:
\(A=\frac{8a^2+b}{4a}+b^2=2a+\frac{b}{4a}+b^2\)
\(\Leftrightarrow A+\frac{1}{4}=2a+\frac{b+a}{4a}+b^2=2a+b+\frac{b+a}{4a}+b^2-b\)
Vì \(a+b\geq 1, a>0\) nên \(A+\frac{1}{4}\geq a+1+\frac{1}{4a}+b^2-b\)
Áp dụng BĐT AM-GM:
\(a+\frac{1}{4a}\geq 2\sqrt{\frac{1}{4}}=1\)
\(\Rightarrow A+\frac{1}{4}\geq 2+b^2-b=\left(b-\frac{1}{2}\right)^2+\frac{7}{4}\geq \frac{7}{4}\)
\(\Leftrightarrow A\geq \frac{3}{2}\).
Vậy \(A_{\min}=\frac{3}{2}\Leftrightarrow a=b=\frac{1}{2}\)

(bài 1) a) \(\dfrac{1}{5+2\sqrt{6}}-\dfrac{1}{5-2\sqrt{6}}\) = \(\dfrac{5-2\sqrt{6}-5-2\sqrt{6}}{25-24}\)
= \(\dfrac{-4\sqrt{6}}{1}\) = \(-4\sqrt{6}\)
b) \(\sqrt{6+2\sqrt{5}}-\dfrac{\sqrt{15}-\sqrt{3}}{\sqrt{3}}\) = \(\sqrt{\left(\sqrt{5}+1\right)^2}-\dfrac{\sqrt{3}\left(\sqrt{5}-1\right)}{\sqrt{3}}\)
= \(\left(\sqrt{5}+1\right)-\left(\sqrt{5}-1\right)\) = \(\sqrt{5}+1-\sqrt{5}+1\) = \(2\)
c) \(\dfrac{3\sqrt{2}-2\sqrt{3}}{\sqrt{3}-\sqrt{2}}:\dfrac{1}{\sqrt{16}}\) = \(\dfrac{\sqrt{6}\left(\sqrt{3}-\sqrt{2}\right)}{\sqrt{3}-\sqrt{2}}:\dfrac{1}{\sqrt{16}}\)
= \(\sqrt{6}.\sqrt{16}\) = \(4\sqrt{6}\)
d) \(\dfrac{3+2\sqrt{3}}{\sqrt{3}}+\dfrac{2+\sqrt{2}}{1+\sqrt{2}}-\dfrac{1}{2-\sqrt{3}}\)
= \(\dfrac{\sqrt{3}\left(\sqrt{3}+2\right)}{\sqrt{3}}+\dfrac{\sqrt{2}\left(\sqrt{2}+1\right)}{1+\sqrt{2}}-\dfrac{1}{2-\sqrt{3}}\)
= \(\sqrt{3}+2+\sqrt{2}-\dfrac{1}{2-\sqrt{3}}\) = \(\dfrac{\left(\sqrt{3}+2+\sqrt{2}\right)\left(2-\sqrt{3}\right)-1}{2-\sqrt{3}}\)
= \(\dfrac{2\sqrt{3}-3+4-2\sqrt{3}+2\sqrt{2}-\sqrt{6}-1}{2-\sqrt{3}}\)
= \(\dfrac{2\sqrt{2}-\sqrt{6}}{2-\sqrt{3}}\) = \(\dfrac{\sqrt{2}\left(2-\sqrt{3}\right)}{2-\sqrt{2}}\) = \(\sqrt{2}\)
e) \(\dfrac{4}{1+\sqrt{3}}-\dfrac{\sqrt{15}+\sqrt{3}}{1+\sqrt{5}}\) = \(\dfrac{4}{1+\sqrt{3}}-\dfrac{\sqrt{3}\left(\sqrt{5}+1\right)}{1+\sqrt{5}}\)
= \(\dfrac{4}{1+\sqrt{3}}-\sqrt{3}\) = \(\dfrac{4-\sqrt{3}-3}{1+\sqrt{3}}\) = \(\dfrac{1-\sqrt{3}}{1+\sqrt{3}}\)
= \(\dfrac{\left(1-\sqrt{3}\right)\left(1-\sqrt{3}\right)}{1-3}\) = \(\dfrac{1-2\sqrt{3}+3}{-2}\) = \(\dfrac{4-2\sqrt{3}}{-2}\)
= \(\dfrac{-2\left(-2+\sqrt{3}\right)}{-2}\) = \(\sqrt{3}-2\)
bài 2)
a)\(\dfrac{a+b-2\sqrt{ab}}{\sqrt{a}-\sqrt{b}}:\dfrac{1}{\sqrt{a}+\sqrt{b}}=\dfrac{\left(a+b-2\sqrt{ab}\right)\left(\sqrt{a}+\sqrt{b}\right)}{\sqrt{a}-\sqrt{b}}\)
= \(\dfrac{a\sqrt{a}+a\sqrt{b}+b\sqrt{a}+b\sqrt{b}-2a\sqrt{b}-2b\sqrt{a}}{\sqrt{a}-\sqrt{b}}\)
= \(\dfrac{a\sqrt{a}+-a\sqrt{b}+b\sqrt{b}-b\sqrt{a}}{\sqrt{a}-\sqrt{b}}\) = \(\dfrac{a\left(\sqrt{a}-\sqrt{b}\right)-b\left(\sqrt{a}-\sqrt{b}\right)}{\sqrt{a}-\sqrt{b}}\)
= \(\dfrac{\left(a-b\right)\left(\sqrt{a}-\sqrt{b}\right)}{\sqrt{a}-\sqrt{b}}\) = \(a-b\)
b) \(\left(\dfrac{\sqrt{a}}{2}-\dfrac{1}{2\sqrt{a}}\right).\left(\dfrac{a-\sqrt{a}}{\sqrt{a}+1}-\dfrac{a+\sqrt{a}}{\sqrt{a}-1}\right)\)
= \(\dfrac{2a-2}{4\sqrt{a}}.\dfrac{\sqrt{a}\left(\sqrt{a}-1\right)^2-\sqrt{a}\left(\sqrt{a}+1\right)^2}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}\)
= \(\dfrac{2a-2}{4\sqrt{a}}.\dfrac{\sqrt{a}\left(a-2\sqrt{a}+1\right)-\sqrt{a}\left(a+2\sqrt{a}+1\right)}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}\)
= \(\dfrac{2a-2}{4\sqrt{a}}.\dfrac{a\sqrt{a}-2a+\sqrt{a}-a\sqrt{a}-2a-\sqrt{a}}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}\)
= \(\dfrac{2\left(a-1\right)}{4\sqrt{a}}.\dfrac{-4a}{a-1}\) = \(-2\)

Ta có \(\sqrt{1+8a^3}=\sqrt{\left(1+2a\right)\left(1-2a+4a^2\right)}\le\frac{1+2a+1-2a+4a^2}{2}=1+2a^2\)(BĐT AM-GM)
Tương tự cho \(\sqrt{1+8b^2};\sqrt{1+8c^2}\)ta được \(P\ge\frac{1}{1+2a^2}+\frac{1}{1+2b^2}+\frac{1}{1+2c^2}\)
Mặt khác \(\frac{1}{1+2a^2}=\frac{1}{1+2a^2}+\frac{1+2a^2}{9}-\frac{1+2a^2}{9}\ge2\sqrt{\frac{1}{1+2a^2}\cdot\frac{1+2a^2}{9}}-\frac{2}{9}a^2-\frac{1}{9}=\frac{5-2a^2}{9}\)
Khi đó: \(P\ge\frac{5-2a^2}{9}-\frac{5-2b^2}{9}-\frac{5-2c^2}{9}\) \(=\frac{15-2\left(a^2+b^2+c^2\right)}{9}=\frac{15-2\cdot3}{9}=1\)
Vậy Min P=1
Dấu "=" xảy ra \(\Leftrightarrow\hept{\begin{cases}a^2+b^2+c^2=3\\1+2a=1-2a+4a^2\\\frac{1}{1+2a^2}=\frac{1+2a^2}{9}\end{cases}}\)và vai trò a,b,c như nhau hay (a,b,c)=(1,1,1)