Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D y 1 2 3 2 1
Vì \(\widehat{B}=\widehat{C}\Rightarrow\Delta ABC\text{ cân tại A }\Rightarrow AB=AC\)
Xét \(\Delta ABD\text{ và }\Delta ADC\) có :
\(\hept{\begin{cases}AB=AC\\\widehat{A_1}=\widehat{A_2}\\AD\text{ chung }\end{cases}\Rightarrow\Delta ABD=\Delta ACD\left(c.g.c\right)}\)
=> \(\widehat{D_1}=\widehat{D_2}\text{ mà }\widehat{D_1}+\widehat{D_2}=180^{\text{o}}\Rightarrow\widehat{D_1}=\widehat{D_2}=90^{\text{o}}\)
Mà Ay//BC
=> \(\widehat{A_{23}}+\widehat{D_2}=180^{\text{o}}\text{ mà }\widehat{D_2}=90^{\text{o}}\Rightarrow\widehat{A_{23}}=90^{\text{o}}\Rightarrow AD\perp Ay\left(\text{đpcm}\right)\)

a) Δ BID và Δ CIA có:
ID=IB (gt)
DIB=CIA (đối đỉnh)
IA=ID (gt)
=> Δ BID=Δ CIA (c.g.c)
b) Ta có: AM // BC
=> MAB=CAB (so le trong)
Δ BID=Δ CIA (cmt)
=> BDI=CAI ( 2 góc tương ứng)
và chúng ở vị trí so le trong
=> CA // DM
Ta có: CA // DM (cmt)
=> CAB=MBA=900 (so le trong)
Δ BAM và Δ ABC có:
MAB=CAB (cmt)
BA cạnh chung
CAB=MBA=900 (cmt)
=> Δ BAM=Δ ABC (g.c.g)
c)Δ BAM=Δ ABC
=> BM=AC (2 cạnh tương ứng)
Mà AC=BD ( Δ BID=Δ CIA)
=>BM=BD
MBA=900 (cmt)
mà MBA+ABD=1800 ( kề bù)
900 +ABD=1800
=>ABD=1800-900=900
=>MBA=ABD
Δ ADB=Δ AMB có:
BM=BD (cmt)
MBA=ABD (cmt)
AB cạnh chung
=> Δ ADB=Δ AMB ( g.c.g)
=>MAB=DAB (2 góc tương ứng)
Vậy AB là phân giác góc DAM
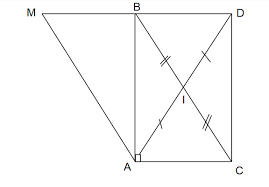
Bạn ơi, vì mình k thể kí hiệu góc. Nên bạn tự ghi góc vào bài làm của mình nhé
Ta có: \(\widehat{DIB}=\widehat{IBC}\)
\(\widehat{DBT}=\widehat{TBC}\)
Do đó: \(\widehat{DIB}=\widehat{DBT}\)