
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

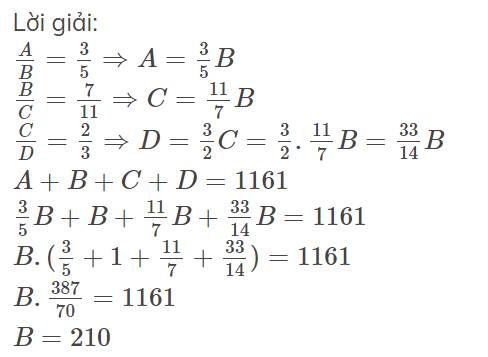

Lời giải:
$\frac{A}{B}=\frac{3}{5}\Rightarrow A=\frac{3}{5}B$
$\frac{B}{C}=\frac{7}{11}\Rightarrow C=\frac{11}{7}B$
$\frac{C}{D}=\frac{2}{3}\Rightarrow D=\frac{3}{2}C=\frac{3}{2}.\frac{11}{7}B=\frac{33}{14}B$
$A+B+C+D=1161$
$\frac{3}{5}B+B+\frac{11}{7}B+\frac{33}{14}B=1161$
$B.(\frac{3}{5}+1+\frac{11}{7}+\frac{33}{14})=1161$
$B.\frac{387}{70}=1161$
$B=210$

\(x^3-5x^2+8x-4.\)
\(=x^3-4x^2-x^2+4x^2+4x^2-4\)
\(=\left(x^3-4x^2+4x\right)-\left(x^2-4x+4\right)\)
\(=x\left(x^2-4x+4\right)-\left(x^2-4x+4\right)\)
\(=\left(x^2-4x+4\right)\left(x-1\right)\)
\(=\left(x-2\right)^2\left(x-1\right)\)
Cảm ơn bạn nhiều
Bạn có thể giúp mình phần còn lại đc hem ? ^.^

Ta có : A = x2 - 4x + 1
=> A = x2 - 2.x.2 + 4 - 3
=> A = (x - 2)2 - 3
Mà : (x - 2)2 \(\ge0\forall x\in R\)
Nên : (x - 2)2 - 3 \(\ge-3\forall x\in R\)
Vậy GTNN của A là -3 khi x = 2
\(B=4x^2+4x+11=\left(2x\right)^2+2.2x.1+1+10=\left(2x+1\right)^2+10\)
Vì \(\left(2x+1\right)^2\ge0\Rightarrow B=\left(2x+1\right)^2+10\ge10\)
Dấu "=" xảy ra khi (2x+1)2=0 <=> 2x+1=0 <=> x=-1/2
Vậy gtnn của B là 10 khi x=-1/2
---
\(C=\left(x-1\right)\left(x+2\right)\left(x+3\right)\left(x+6\right)=\left(x^2+5x-6\right)\left(x^2+5x+6\right)=\left(x^2+5x\right)^2-36\ge-36\)
Dấu "=" xảy ra khi x=0 hoặc x=-5

Bài 1:
\(\left\{{}\begin{matrix}a=5c+1\\b=5d+2\end{matrix}\right.\)
\(a^2+b^2=\left(5c+1\right)^2+\left(5d+2\right)^2\)
\(=25c^2+10c+1+25d^2+20d+4\)
\(=25c^2+25d^2+10c+20d+5\)
\(=5\left(5c^2+5d^2+2c+4d+1\right)⋮5\)
Bài 3:
a: \(4x^2+12x+15=4x^2+12x+9+6=\left(2x+3\right)^2+6>=6\forall x\)
Dấu '=' xảy ra khi x=-3/2
b: \(9x^2-6x+5=9x^2-6x+1+4=\left(3x-1\right)^2+4>=4\forall x\)
Dấu '=' xảy ra khi x=1/3

a: Để A là số nguyên thì \(x^3-3x^2-x^2+3x+x-3-7⋮x-3\)
\(\Leftrightarrow x-3\in\left\{1;-1;7;-7\right\}\)
hay \(x\in\left\{4;2;10;-4\right\}\)
b: Đề sai rồi bạn