Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi \(n_{Mg} = a(mol) ; n_{Al} = b(mol)\\ \Rightarrow 24a + 27b = 5,7(1)\)
\(Mg^0 \to Mg^{+2} + 2e\\ Al^0 \to Al^{+3} + 3e\\ O_2 + 4e \to 2O^{-2}\\ Cl_2 + 2e \to 2Cl^-\)
Bảo toàn electron : \(2n_{Mg} + 3n_{Al} = 2a + 3b = 4n_{O_2} + 2n_{Cl_2} = 1,2(mol)\)(2)
Từ (1)(2) suy ra : a = -0,85< 0 ⇒ Sai đề
X{Mg, Al} + {Cl2, O2} → Z
Áp dụng định luật BTKL: mCl2 + mO2 = mZ – mX = 19,7 – 7,8 = 11,9 gam
Theo đề bài ta có hệ phương trình:
⎧⎪⎨⎪⎩nCl2+nO2=5,622,4=0,2571nCl2+32nO2=11,9→{nCl2=0,1nO2=0,15{nCl2+nO2=5,622,4=0,2571nCl2+32nO2=11,9→{nCl2=0,1nO2=0,15
Đặt số mol của Mg và Al lần lượt là x và y (mol)
- Khối lượng hỗn hợp: 24x + 27y = 7,8 (1)
- Bảo toàn e: 2nMg + 3nAl = 2nCl2 + 4nO2 => 2x + 3y = 0,1.2 + 0,15.4 hay 2x + 3y = 0,8 (2)
Giải (1) và (2) thu được x = 0,1 và y = 0,2
=> %mAl = 0,2.27/7,8 = 69,23%

- Từ giả thiết tính được : n Cl 2 = 0,035 mol; n O 2 = 0,025 mol
Theo ĐLBT khối lượng :
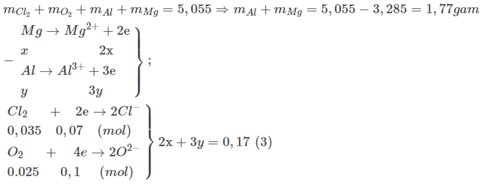
Từ (3)(4) ⇒ x = 0,04; y = 0,03
⇒ m Mg = 0,04.24 = 0,96g; m Al = 0,03.27 = 0,81g
Phản ứng không oxi hoá - khử

X + Y → Z
Bảo toàn khối lượng → mX + mY = mZ
→ mX + 11,1 = 30,1
→ mX = 19 gam
Giả sử X chứa a mol Cl2 và b mol O2
Ta có hệ pt:
\(\left\{{}\begin{matrix}n_X=a+b=\frac{7,84}{22,4}=0,35\\m_X=71a+32b=19\end{matrix}\right.\rightarrow\left\{{}\begin{matrix}a=0,2\\b=0,15\end{matrix}\right.\)
Giả sử Y chứa u mol Mg và v mol Al
→ mY = 24u + 27v = 11,1 (1)
Quá trình cho - nhận e:
Mg0 → Mg+2 + 2e __________Cl2 + 2e → 2Cl-
Al0 → Al+3 + 3e_____________O2 + 4e → 2O-2
Áp dụng bảo toàn e: 2nMg + 3nAl = 2nCl2 + 4nO2
→ 2u + 3v = 2.0,2 + 4.0,15 (2)
Giải (1) (2) được u = 0,35 và v = 0,1
\(\%m_{Mg}=\frac{0,35.24}{11,1}.100\%=75,7\%\)
\(\%m_{Al}=100\%-75,7\%=24,3\%\)

24nMg + 64nCu = 8,8 (1)
Ta có: nCl2 = 0,2 (mol)
BT e, có: 2nMg + 2nCu = 2nCl2 = 0,4 (2)
Từ (1) và (2) ⇒ nMg = nCu = 0,1 (mol)
⇒ mMg = 0,1.24 = 2,4 (g)
mCu = 0,1.64 = 6,4 (g)

Số k đẹp lắm nên đã làm tròn rồi nha :)
\(BTKL:m_A=13,86-10,76=3,1\left(g\right)\)
Đặt \(n_{Cl_2}=x\left(mol\right);n_{Br_2}=y\left(mol\right)\)
Theo đề ta có hệ \(\left\{{}\begin{matrix}\frac{x}{y}=\frac{3}{2}\\71x+160y=10,76\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0,06\\y=0,04\end{matrix}\right.\)
Đặt \(n_{Mg}=a\left(mol\right);n_{Fe}=b\left(mol\right)\)
\(BTe:2a+3b=0,06.2+0,04.2=0,2\)
Theo đề ta có hệ \(\left\{{}\begin{matrix}24a+56b=3,1\\2a+3b=0,2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=0,0475\\b=0,035\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\%m_{Mg}=\frac{0,0475.24}{3,1}.100\%=36,8\%\\\%m_{Fe}=100-36,8=63,2\%\end{matrix}\right.\)

Đáp án B
Có:
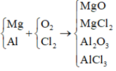
Áp dụng định luật bảo toàn khối lượng ta có:
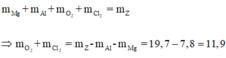
Gọi
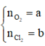
Có:
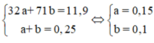
Gọi
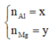
Có
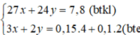
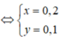
Vậy
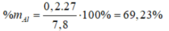

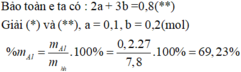
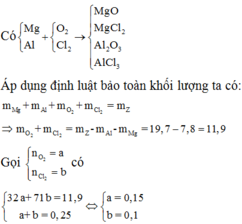
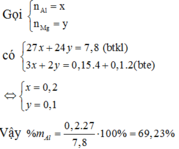
Gọi số mol Al, Mg lần lượt là: x, y (mol)
=> 27x + 24y = 9 (*)
Ta có: \(\overset{0}{Al}\rightarrow\overset{+3}{Al}+3e\)
x \(\rightarrow\) 3x (mol)
\(\overset{0}{Mg}\rightarrow\overset{+2}{Mg}+2e\)
y \(\rightarrow\) 2y (mol)
\(\overset{0}{O_2}+4e\rightarrow\overset{-2}{2O}\)
0,1\(\rightarrow\) 0,4 (mol)
\(\overset{0}{Cl_2}+2e\rightarrow\overset{-1}{2Cl}\)
0,25 \(\rightarrow\) 0,5 (mol)
Theo ĐLBT e, ta có: 3x +2y = 0,9 (**)
Từ (*) và (**), có: \(\left\{{}\begin{matrix}x=0,2\left(mol\right)\\y=0,15\left(mol\right)\end{matrix}\right.\)
=> mAl = 5,4 (g) => %mAl = 60%
=> %mMg = 40 %