Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải:
Vì \(0\leq a,b,c\leq 1\Rightarrow ab,ac,ab\geq abc\)
Do đó mà \(\frac{a}{bc+1}+\frac{b}{ac+1}+\frac{c}{ab+1}\leq \frac{a+b+c}{abc+1}\)
Giờ chỉ cần chỉ ra \(\frac{a+b+c}{abc+1}\leq 2\). Thật vậy:
Do \(0\leq b,c\leq 1\Rightarrow (b-1)(c-1)\geq 0\Leftrightarrow bc+1\geq b+c\Rightarrow bc+a+1\geq a+b+c\)
Suy ra \( \frac{a+b+c}{abc+1}\leq \frac{bc+a+1}{abc+1}=\frac{bc+a-2abc-1}{abc+1}+2=\frac{(bc-1)(1-a)-abc}{abc+1}+2\)
Ta có \(\left\{\begin{matrix}bc\le1\\a\le1\\abc\ge0\end{matrix}\right.\Rightarrow\left\{\begin{matrix}\left(bc-1\right)\left(1-a\right)\le1\\-abc\le0\end{matrix}\right.\) \(\Rightarrow \frac{(bc-1)(1-a)-abc}{abc+1}+2\leq 2\Rightarrow \frac{a+b+c}{abc+1}\leq 2\)
Chứng minh hoàn tất
Dấu bằng xảy ra khi \((a,b,c)=(0,1,1)\) và hoán vị.

Đáp án là B.
+ log a b = 2 log b c log b c = 2 log c a
⇒ log 2 b c = log c b ⇔ log 3 b c = 1 ⇔ c = b , 1
+ log b c . log a c = 2 , 2
Từ (1) và (2) ⇒ c = a 2 3 .
+ Thay (1);(2) và (3) vào:
a + 2 b + 3 c = 48 ⇒ a = 3 ; b = c = 9
Vậy P = a b c = 243.

Đáp án B.
Từ
f x . f ' x = 2 x f 2 x + 1 ⇒ f x . f ' x f 2 x + 1 = 2 x ⇒ ∫ f x . f ' x f 2 x + 1 d x = ∫ 2 x d x
(1)
Đặt
f 2 x + 1 = t ⇒ f 2 x = t 2 − 1 ⇒ 2 f x . f ' x d x = 2 t d t ⇒ f x . f ' x d x = t d t
Suy ra ∫ f x . f ' x f 2 x + 1 x = ∫ t d t t = ∫ d t = t + C 1 = f 2 x + 1 + C 1 và ∫ 2 x d x = x 2 + C 2
Từ (1) ta suy ra f 2 x + 1 + C 1 = x 2 + C 2 . Do f 0 = 0 nên C 2 − C 1 = 1 .
Như vậy
f 2 x + 1 = x 2 + C 2 − C 1 = x 2 + 1 ⇒ f 2 x = x 2 + 1 2 − 1 = x 4 + 2 x 2
⇒ f x = x 4 + 2 x 2 = x x 2 + 2 = x x 2 + 2
(do x ∈ 1 ; 3 ).
Ta có f ' x = x 2 + 2 + x 2 x 2 + 2 = 2 x 2 + 1 x 2 + 2 > 0, ∀ x ∈ ℝ ⇒ Hàm số f x = x x 2 + 2 đồng biến trên R nên f x cũng đồng biến trên 1 ; 3 .
Khi đó M = max 1 ; 3 f x = f 3 = 3 11 và m = min 1 ; 3 f x = f 1 = 3 .
Vậy
P = 2 M − m = 6 11 − 3 ⇒ a = 6 ; b = 1 ; c = 0 ⇒ a + b + c = 7

Nhận thấy các đáp án đều có tích xy nên ta sẽ tính tích này.
Ta có ![]()

Chọn C.
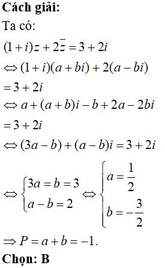

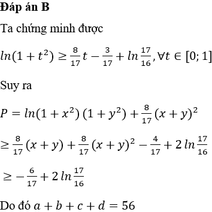

Lời giải:
Từ điều kiện đề bài ta có:
\(\frac{c-1}{c}=1-\frac{1}{c}=\frac{1}{a}+\frac{1}{b}=\frac{a+b}{ab}=\frac{1-c}{ab}\) \(\Leftrightarrow (c-1)\left(\frac{1}{c}+\frac{1}{ab}\right)=0\)
\(\Leftrightarrow (c-1)\left(\frac{1}{1-a-b}+\frac{1}{ab}\right)=\frac{(a-1)(b-1)(c-1)}{abc}=0\)
Do đó tồn tại ít nhất một trong các số đã cho có giá trị bằng $1$