Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
b: \(AB=\sqrt{\left(-2-2\right)^2+\left(0-1\right)^2}=\sqrt{17}\)
\(AC=\sqrt{\left(3-2\right)^2+\left(3-1\right)^2}=\sqrt{5}\)
\(BC=\sqrt{\left(3+2\right)^2+\left(3-0\right)^2}=\sqrt{34}\)
\(cosA=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{-6}{\sqrt{85}}\)
=>sin A=7/căn 85
\(S_{ABC}=\dfrac{1}{2}\cdot\sqrt{17}\cdot\sqrt{5}\cdot\dfrac{7}{\sqrt{85}}=\dfrac{7}{2}\)
\(AD=\sqrt{\left(4-2\right)^2+\left(5-1\right)^2}=2\sqrt{5}\)
\(DE=\sqrt{\left(-9-4\right)^2+\left(4-5\right)^2}=\sqrt{170}\)
\(AE=\sqrt{\left(-9-2\right)^2+\left(4-1\right)^2}=\sqrt{178}\)
\(cosA=\dfrac{AD^2+AE^2-DE^2}{2\cdot AD\cdot AE}\simeq0,23\)
=>sin A=0,97
\(S_{ADE}=\dfrac{1}{2}\cdot2\sqrt{5}\cdot\sqrt{178}\cdot0,97=29\)
\(OA=\sqrt{2^2+1^2}=\sqrt{5};OB=\sqrt{\left(-2\right)^2}=2\)
AB=căn 17
\(cosA=\dfrac{AO^2+AB^2-OB^2}{2\cdot AO\cdot AB}=\dfrac{9}{\sqrt{85}}\)
=>sin A=2/căn 85
\(S_{OAB}=\dfrac{1}{2}\cdot\sqrt{5}\cdot\sqrt{17}\cdot\dfrac{2}{\sqrt{85}}=1\)
c: vecto AB=(-4;-1)=(4;1)
Tọa độ M là trung điểm của AB là;
x=(2-2)/2=0 và y=(1+0)/2=0,5
Phương trình trung trực của AB là:
4(x-0)+1(y-0,5)=0
=>4x+y-0,5=0
vecto AC=(1;2)
Tọa độ trung điểm của AC là;
x=(2+3)/2=2,5 và y=(1+3)/2=2
Phương trình trung trực của AC là:
1(x-2,5)+2(y-2)=0
=>x+2y-6,5=0
vecto BC=(5;3)
Tọa độ trung điểm của BC là:
x=(-2+3)/2=1/2 và y=(0+3)/2=1,5
Phương trình trung trực của BC là:
5(x-0,5)+3(y-1,5)=0
=>5x+3y-4=0
5:
Gọi (d): y=ax+b là phương trình cần tìm
Theo đề, ta có hệ:
3a+b=-1 và 2a+b=3
=>a=-4 và b=11
=>y=-4x+11
4:
vecto BC=(1;-1)
=>AH có VTPT là (1;-1)
Phương trình AH là:
1(x-1)+(-1)(y+3)=0
=>x-1-y-3=0
=>x-y-4=0
a: vecto BC=(1;-3)
=>VTPT là (3;1)
Phương trình BC là:
3(x-2)+y-2=0
=>3x-6+y-2=0
=>3x+y-8=0
b: Phương trình AH nhận vecto BC làm VTPT
=>Phương trình AH là:
1(x-1)+(-3)*(y-1)=0
=>x-1-3y+3=0
=>x-3y+2=0
c: Tọa độ M là:
\(\left\{{}\begin{matrix}x=\dfrac{1+3}{2}=2\\y=\dfrac{1-1}{2}=0\end{matrix}\right.\)
M(2;0); B(2;2)
vecto BM=(0;-2)
=>VTPT là (2;0)
Phương trình BM là:
2(x-2)+0(y-0)=0
=>2x-4=0
=>x=2
a) Viết phương trình tổng quát của AB và tính diện tích tam giác ABC
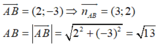
Phương trình tổng quát của AB là: 3(x - 1) + 2(y - 2) = 0 ⇔ 3x + 2y - 7 = 0
Kẻ CH ⊥ AB, (H ∈ AB)
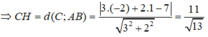
Diện tích tam giác ABC là:
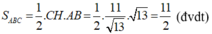
b) Viết phương trình đường tròn đường kính AB
Gọi I là trung điểm của AB
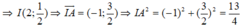
Đường tròn đường kính AB là đường tròn tâm I bán kính IA:
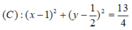
a: vecto AB=(1;-1); vecto AC=(2;1); vecto BC=(1;2)
AB có VTPT là (1;1)
Phương trình AB là;
1(x-1)+1(y+1)=0
=>x+y=0
AC có VTPT là (-1;2)
PT AC là:
-1(x-1)+2(y+1)=0
=>-x+1+2y+2=0
=>-x+2y+3=0
BC có VTPT là (-2;1)
PT BC là;
-2(x-2)+1(y+2)=0
=>-2x+y+6=0
b: AH có VTPT là (1;2)
Phương trình AH là:
1(x-1)+2(y+1)=0
=>x-1+2y+2=0
=>x+2y+1=0
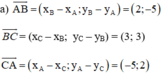
+ Lập phương trình đường thẳng AB:
Đường thẳng AB nhận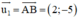 
là 1 vtcp ⇒ AB nhận 
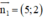là 1 vtpt
Mà A(1; 4) thuộc AB
⇒ PT đường thẳng AB: 5(x- 1) + 2(y – 4) = 0 hay 5x + 2y – 13 = 0.
+ Lập phương trình đường thẳng BC:
Đường thẳng BC nhận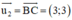 
là 1 vtcp ⇒ BC nhận 
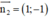là 1 vtpt
Mà B(3; –1) thuộc BC
⇒ Phương trình đường thẳng BC: 1(x - 3) – 1(y + 1) = 0 hay x – y – 4 = 0.
+ Lập phương trình đường thẳng CA:
Đường thẳng CA nhận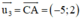 
là 1 vtcp ⇒ CA nhận 
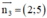là 1 vtpt
Mà C(6; 2) thuộc CA
⇒ Phương trình đường thẳng AC: 2(x – 6) + 5(y - 2) = 0 hay 2x + 5y – 22 = 0.
b) + AH là đường cao của tam giác ABC ⇒ AH ⊥ BC
⇒ Đường thẳng AH nhận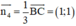 
là 1 vec tơ pháp tuyến
Mà A(1; 4) thuộc AH
⇒ Phương trình đường thẳng AH: 1(x - 1) + 1(y - 4) = 0 hay x + y – 5 = 0.
+ Trung điểm M của BC có tọa độ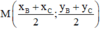 
hay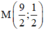 
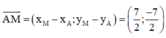
Đường thẳng AM nhận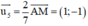 
là 1 vtcp
⇒ AM nhận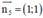 
là 1 vtpt
Mà A(1; 4) thuộc AM
⇒ Phương trình đường thẳng AM: 1(x - 1) + 1(y – 4) = 0 hay x + y – 5 = 0.
Ta có = (2; -5). Gọi M(x; y) là 1 điểm nằm trên đường thẳng AB thì AM = (x – 1; y – 4). Ba điểm A, B, M thẳng hàng nên hai vec tơ
và
cùng phương, cho ta:
=
<=> 5x + 2y -13 = 0
Đó chính là phương trình đường thẳng AB.
Tương tự ta có phương trình đường thẳng BC: x – y -4 = 0
phương trình đường thẳng CA: 2x + 5y -22 = 0
b) \(AB=\sqrt{\left(-4-0\right)^2+\left(1-2\right)^2}=\sqrt{17}\)
\(AC=\sqrt{\left(-4-3\right)^2+\left(1+1\right)^2}=\sqrt{53}\)
\(BC=\sqrt{\left(0-3\right)^2+\left(2+1\right)^2}=3\sqrt{2}\)
Nửa chu vi là:
\(P=\dfrac{AB+BC+AC}{2}=\dfrac{\sqrt{17}+\sqrt{53}+3\sqrt{2}}{2}\)
Diện tích là:
\(S=\sqrt{P\cdot\left(P-AB\right)\cdot\left(P-AC\right)\cdot\left(P-BC\right)}\)
\(=\sqrt{\dfrac{\sqrt{17}+\sqrt{53}+3\sqrt{2}}{2}\cdot\dfrac{-\sqrt{17}+\sqrt{53}+3\sqrt{2}}{2}\cdot\dfrac{\sqrt{17}-\sqrt{53}+3\sqrt{2}}{2}\cdot\dfrac{\sqrt{17}+\sqrt{53}-3\sqrt{2}}{2}}\)
\(=\dfrac{15}{2}\left(đvdt\right)\)