
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

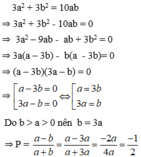

\(B=\frac{16}{\left(a-b\right)\left(a+b\right)}\)
Ta có : \(a^2+2ab+b^2=10+2ab=16\)
<=>\(\left(a+b\right)^2=16\) Vì a, b đều dương nên ta có : \(a+b=4\)
Mặt khác ta lại có : \(a^2-2ab+b^2=10-2ab=4\)
<=> \(\left(a-b\right)^2=4\)<=> \(\orbr{\begin{cases}a-b=4\\a-b=-4\end{cases}}\)
=> Bạn thay vào B tính nha



\(a^2+b^2-2ab=13-2.6=1=\left(a-b\right)^2\)
\(\Rightarrow\orbr{\begin{cases}a-b=1\\a-b=-1\end{cases}}\)
\(A=a^3-b^3=\left(a-b\right)\left(a^2+ab+b^2\right)\)
Với \(a-b=1\)
\(\Rightarrow A=1.\left(13+6\right)=19\)
Với \(a-b=-1\)
\(\Rightarrow A=-1\left(13+6\right)=-19\)
Vậy \(\orbr{\begin{cases}A=19\\A=-19\end{cases}}\)
b ) \(a^2+b^2+2ab=13+2.6=25=\left(a+b\right)^2\)
\(\Rightarrow\orbr{\begin{cases}a+b=5\\a+b=-5\end{cases}}\)
\(B=a^2-b^2=\left(a-b\right)\left(a+b\right)\)
Với \(a-b=1;a+b=5\Rightarrow B=1.5=5\)
Với \(a-b=1;a+b=-5\Rightarrow B=1.-5=-5\)
Tương tự với \(\hept{\begin{cases}a-b=-1;a+b=-5\\a-b=-1;a+b=5\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}B=5\\B=-5\end{cases}}\)
Vậy ...
Chúc bạn học tốt !!!
Làm lại :
a ) Do \(a>b>0\)
\(\Rightarrow a-b>0\)
\(a^2+b^2-2ab=13-2.6=1=\left(a-b\right)^2\)
\(\Rightarrow a-b=1\)
\(A=a^3-b^3=\left(a-b\right)\left(a^2+ab+b^2\right)\)
\(\Rightarrow A=1.\left(13+6\right)=19\)
Vậy \(A=19\)
b ) \(B=a^2-b^2=\left(a-b\right)\left(a+b\right)=1\left(a+b\right)=a+b\)
Do \(a>b>0\Rightarrow a+b>0\)
\(a^2+b^2+2ab=13+2.6=25=\left(a+b\right)^2\)
\(\Rightarrow a+b=5\)
Mà \(B=a+b\)
\(\Rightarrow B=5\)
Vậy \(B=5\)


Có: \(a^2+b^2=1-2ab\)
\(\Rightarrow a^2+b^2+2ab=1\Rightarrow\left(a+b\right)^2=1\)
Mà: \(a>0;b>0\Rightarrow a+b>0\)
Do đó: \(a+b=1\)
Có: \(M=a^3+b^3+3ab=a^3+b^3+3ab\left(a+b\right)=\left(a+b\right)^3=1^3=1\)
Ta có : M=a3+b3+3ab
=(a+b)(a2-ab+b2)+3ab=(a+b)(a2+b2-ab)+3ab
Ma : a2+b2=1-2ab
\(\Rightarrow\)(a+b)(a2+b2-ab)+3ab
=(a+b)(1-2ab-ab)+3ab
=(a+b)(1-3ab)+3ab
=a+b
Ma : a và b là hai số dương \(\Rightarrow\)a>0 va b>0
\(\Rightarrow\)Gia tri cua bieu thuc M=a3+b3+3ab = a+b .