
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
2D
1

Các câu hỏi dưới đây có thể giống với câu hỏi trên
NP
1

20 tháng 5 2019
\(M=8x^3+27y^3+4x^2+9y^2+5\)
\(=\left(2x+3y\right)\left(4x^2-6xy+9y^2\right)+4x^2+9y^2+5\)
\(=\left(2x+3y\right)\left(4x^2-6xy+9y^2\right)+4x^2+9y^2+5\)
\(=4x^2-6xy+9y^2+4x^2+9y^2+5\)
Áp dụng BĐT AM-GM có:
\(1\ge2.\sqrt{6xy}\)
\(\Leftrightarrow xy\le\frac{1}{24}\)
Dấu " = " xảy ra <=> 2x=3y <=> x=0,25 y=1/6
Áp dụng BĐT Cauchy-schwarz ta có:
\(M\ge\frac{2.\left(2x+3y\right)^2}{2}-6xy+5\ge\frac{2}{2}-\frac{6.1}{24}+5=6.25\)
Dấu " = " xảy ra <=> 2x=3y <=> x=0,25 y=1/6
KL:.....................................................................
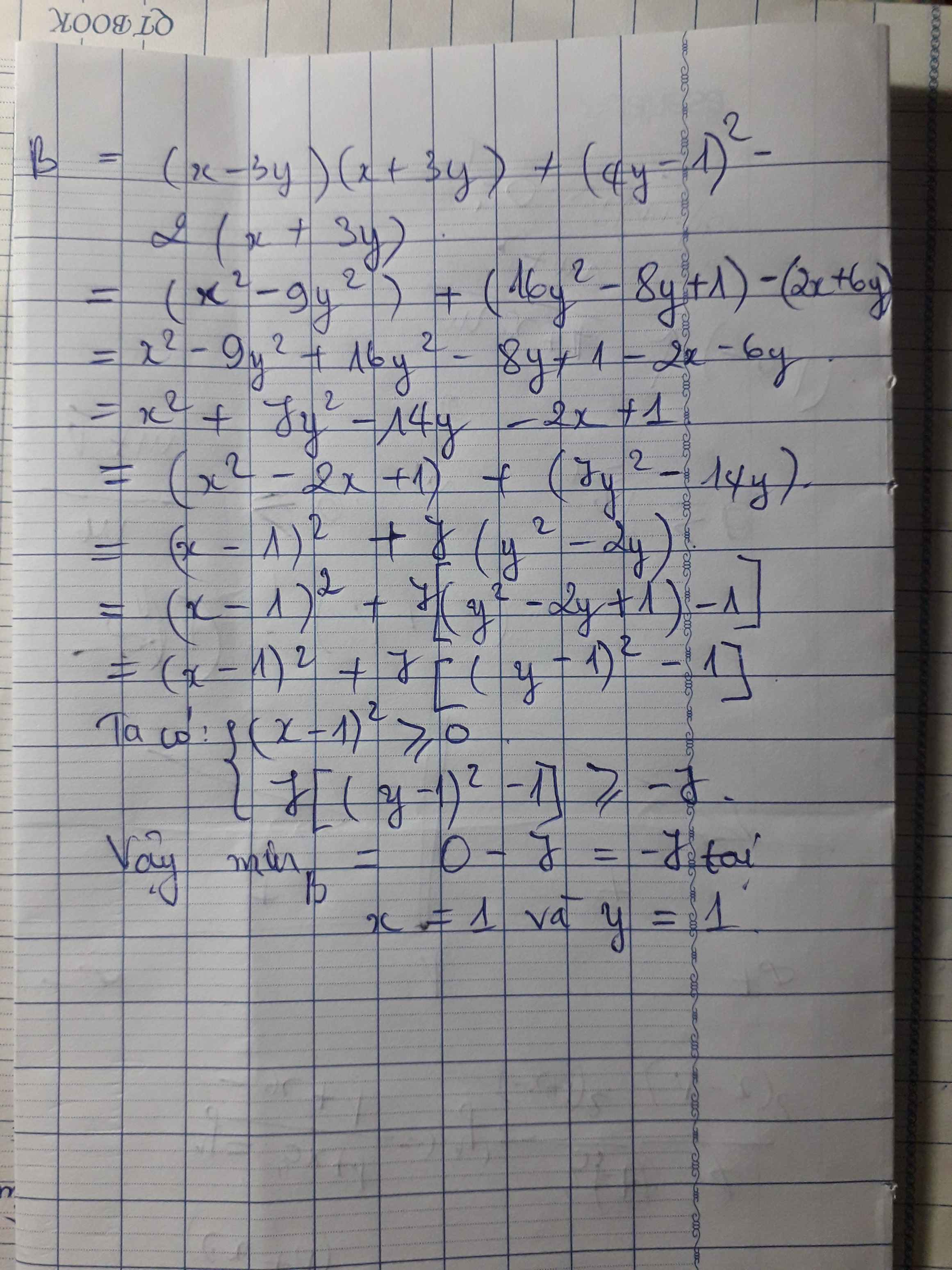
B = x2 + 9y2 + 2011
= x2 + (3y)2 + 2011
= x2 + (5 - 2x)2 + 2011 (do 2x + 3y = 5)
= x2 + 4x2 - 20x + 25 + 2011
= 5x2 - 20x + 2036
= 5x2 - 20x + 20 + 2016
= 5(x2 - 4x + 4) + 2016
= 5(x - 2)2 + 2016 \(\ge2016\)
=> Min B = 2016 khi x - 2 = 0 <=> x = 2
khi đó y = \(\dfrac{1}{3}\)
Vậy Bmin = 2016 khi x = 2 ; \(y=\dfrac{1}{3}\)