Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

c) Giả sử đường thẳng d 1 luôn đi qua một điểm cố định ( x 1 ; y 1 ) với mọi giá trị của m.
⇒ y 1 = m x 1 + 2m - 1 với mọi m
⇔ m( x 1 + 2) - 1 - y 1 = 0 với mọi m
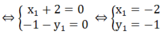
Vậy điểm cố định mà d 1 luôn đi qua với mọi giá trị của m là (-2; -1).

a: Để (d) cắt (d1) tại một điểm trên trục tung thì
\(\left\{{}\begin{matrix}m-2\ne2\\-2m+1=m+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m\ne4\\-3m=1\end{matrix}\right.\Leftrightarrow m=-\dfrac{1}{3}\)
b: Tọa độ giao điểm của d1 và d2 là:
\(\left\{{}\begin{matrix}x+2=4-3x\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x=2\\y=x+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=\dfrac{1}{2}+2=\dfrac{5}{2}\end{matrix}\right.\)
Thay x=1/2 và y=5/2 vào (d), ta được:
\(\dfrac{1}{2}\left(m-2\right)+2+m=\dfrac{5}{2}\)
=>\(\dfrac{1}{2}m-1+m+2=\dfrac{5}{2}\)
=>\(\dfrac{3}{2}m=\dfrac{3}{2}\)
=>m=1
c: (d): y=(m-2)x+m+2
=mx-2x+m+2
=m(x+1)-2x+2
Tọa độ điểm cố định mà (d) luôn đi qua là:
\(\left\{{}\begin{matrix}x+1=0\\y=-2x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=-2\cdot\left(-1\right)+2=4\end{matrix}\right.\)

a, - Để 2 đường thẳng trên vuông góc với nhau thì :
\(\frac{1}{m}.\left(-m\right)=-1\)
=> \(-1=-1\) ( luôn đúng với mọi m, \(m\ne0\) )
Vậy (d1 ) và (d2 ) luôn vuông góc với nhau với mọi giá trị m ≠ 0 .
b, - Gỉa sử đường thẳng (d1 ) luôn đi qua điểm \(A\left(x_0,y_0\right)\) với mọi \(m\ne0\)
=> \(y_0=-mx_0+m+1\)
=> \(y_0-1=m\left(1-x_0\right)\)
=> \(\left\{{}\begin{matrix}y_0-1=0\\1-x_0=0\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}x_0=1\\y_0=1\end{matrix}\right.\)
Vậy điểm cố định (d1) luôn đi qua là điểm ( 1, 1 ) .
Nguyễn Ngọc Lộc ?Amanda?Nguyễn Lê Phước ThịnhPhạm Lan HươngTrần Quốc KhanhAkai HarumaHoàng Thị Ánh Phương Trên con đường thành công không có dấu chân của kẻ lười biếngTrung NguyenHy MinhKhánh LinhVũ Minh Tuấn@Mysterious Person giúp e với e cảm ơn trc

GIẢI HỆ CỦA d1,d2 tìm tọa độ giao điểm giả sử gọi là A
\(\hept{\begin{cases}x-2y=-6\\2x+y=8\end{cases}}\Rightarrow\hept{\begin{cases}2x-4y=-12\\2x+y=8\end{cases}}\Rightarrow5y=20\Rightarrow y=4\Rightarrow x=2y-6=2.4-6=2\)
toạn độ A(2,4) Thay vào phương trinh d có
\(VT=\left(m+2\right)2-\left(2m-1\right)4+6m-8\)
\(=2m+4-8m+4+6m-8\)
\(=8m-8m+8-8=0=VP\forall m\)
vậy đường thẳng d luôn đi qua giao điểm A với mọi m

a: Tọa độ giao điểm của (D1) và (D2) là:
\(\left\{{}\begin{matrix}-x+1=x-3\\y=x-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=-1\end{matrix}\right.\)
b: Thay x=2 và y=-1 vào (D3),ta được:
\(\dfrac{2m+2}{m-1}+\dfrac{2m+1}{m-1}=-1\)
=>4m+3=-m+1
=>5m=-2
hay m=-2/5