Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: A(2;4); B(1;0); C(2;2)
vecto AB=(-1;-4)
vecto DC=(2-x;2-y)
Vì ABCD là hình bình hành nên vecto AB=vecto DC
=>2-x=-1 và 2-y=-4
=>x=3 và y=6
c: N đối xứng B qua C
=>x+1=4 và y+0=4
=>x=3 và y=4

a) ta có : \(\overrightarrow{AB}=\left(2;6\right);\overrightarrow{AC}=\left(-1;7\right)\)
Ta thấy : \(\dfrac{2}{-1}\ne\dfrac{6}{7}\)
=> \(\overrightarrow{AB},\overrightarrow{AC}\) không cùng phương
=> A,B,C là 3 điểm của 1 tam giác
b) Gọi I (x;y) là tọa độ trung điểm AB và G (a;b) là tọa độ trọng tâm tam giác ABC
Ta có : \(\left\{{}\begin{matrix}x=\dfrac{1+3}{2}\\y=\dfrac{-2+4}{2}\end{matrix}\right.=>\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)Vậy I ( 2;1)
Ta có : \(\left\{{}\begin{matrix}a=\dfrac{1+3}{3}\\b=\dfrac{-2+4+5}{3}\end{matrix}\right.=>\left\{{}\begin{matrix}a=\dfrac{4}{3}\\b=\dfrac{7}{3}\end{matrix}\right.\)Vậy G (4/3';7/3)
Gọi D( i;f ) là điểm đối xứng vs b qua C
nên C là trung điểm BD
Ta có : \(\left\{{}\begin{matrix}0=\dfrac{3+i}{2}\\5=\dfrac{4+f}{2}\end{matrix}\right.=>\left\{{}\begin{matrix}i=-3\\f=6\end{matrix}\right.\)
vậy D ( -3;6)

I là trung điểm AJ \(\Rightarrow\left\{{}\begin{matrix}x_A=2x_I-x_J=4\\y_A=2y_I-y_J=-10\end{matrix}\right.\) \(\Rightarrow A\left(4;-10\right)\)
J là trung điểm IB \(\Rightarrow\left\{{}\begin{matrix}x_B=2x_J-x_I=-5\\y_B=2y_J-y_I=11\end{matrix}\right.\) \(\Rightarrow B\left(-5;11\right)\)
a/ B là trung điểm II' \(\Rightarrow\left\{{}\begin{matrix}x_{I'}=2x_B-x_I=-11\\y_{I'}=2y_B-y_I=25\end{matrix}\right.\) \(\Rightarrow I'\left(-11;25\right)\)
b/ K là trung điểm AC \(\Rightarrow\left\{{}\begin{matrix}x_C=2x_K-x_A=\\y_C=2y_K-y_A=\end{matrix}\right.\)
Tương tự K là trung điểm BD \(\Rightarrow\left\{{}\begin{matrix}x_D=2x_K-x_B=\\y_D=2y_K-y_B=\end{matrix}\right.\)
c/ Gọi \(N\left(x;y\right)\Rightarrow\overrightarrow{MN}=\left(x-2;y-4\right)\) ; \(\overrightarrow{AB}=\left(-9;21\right)\)
Do ABMN là hình thang có 2 đáy MN=2AB
\(\Rightarrow\left[{}\begin{matrix}\overrightarrow{MN}=2\overrightarrow{AB}\\\overrightarrow{MN}=-2\overrightarrow{AB}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\left(x-2;y-4\right)=\left(-18;42\right)\\\left(x-2;y-4\right)=\left(18;-42\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}N\left(-16;46\right)\\N\left(20;-38\right)\end{matrix}\right.\)

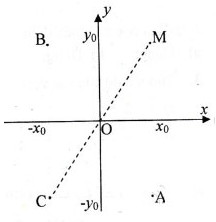
a) Hai điểm đối xứng nhau qua trục hoành thì có hoành độ bằng nhau và tung độ đối nhau.
M0 (x0; y0)=> A(x0;-y0)
b) Hai điểm đối xứng với nhau qua trục tung thì có tung độ bằng nhau còn hoành độ thì đối nhau.
M0 (x0; y0) => B(-x0;y0)
c) Hai điểm đối xứng nhau qua gốc O thì các tọa độ tương ứng đối nhau.
M0 (x0; y0) => C(-x0;-y0)

a) A(3;-5) ; B(1;0)
=> \(\overrightarrow{AB}\left(-2;5\right)\)
Gọi C(x;y) tọa độ cần tìm
khi đó \(\overrightarrow{OC}\left(x;y\right)\)
\(\overrightarrow{OC}=-3\overrightarrow{AB}\Leftrightarrow\left\{{}\begin{matrix}x=-3.\left(-2\right)=6\\y=-3.5=-15\end{matrix}\right.\)
Vậy C(6;-15)
b) D đối xứng với A qua C
=> C trung điểm AD
Gọi D(x1;y1)
Ta có : \(6=\dfrac{3+x_1}{2}\Leftrightarrow x_1=9\)
\(-15=\dfrac{-5+y_1}{2}\) <=> y1 = -25
Vậy D(9;-25)

Bài 1:
a: \(\overrightarrow{AD}=\left(x+1;y-2\right)\)
\(\overrightarrow{BD}=\left(x-3;y+4\right)\)
\(\overrightarrow{CD}=\left(x-5;y\right)\)
Theo đề, ta có:
\(\left\{{}\begin{matrix}x+1-2\left(x-3\right)+3\left(x-5\right)=0\\y-2-2\left(y+4\right)+3y=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-1-2x+6+3x-15=0\\4y-2-2y-8=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x-8=0\\2y-10=0\end{matrix}\right.\)
=>x=4; y=5
b: \(\overrightarrow{AB}=\left(4;-6\right)\)
\(\overrightarrow{BC}=\left(2;4\right)\)
\(\overrightarrow{AD}=\left(x+1;y-2\right)\)
\(\overrightarrow{BD}=\left(x-3;y+4\right)\)
Theo đề, ta có: \(\left\{{}\begin{matrix}x+1-2\cdot4=2\left(x-3\right)+2\\y-2-2\cdot\left(-6\right)=2\left(y+4\right)+4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-7=2x-4\\y-2+12=2y+8+4\end{matrix}\right.\)
=>-x=3 và y+10=2y+12
=>x=-3 và -y=2
=>x=-3 và y=-2
c: ABCD là hình bình hành
nên vecto AB=vecto DC
vecto AB=(4;-6)
vecto DC=(x-5;y)
=>4=x-5 và y=-6
=>x=9 và y=-6

a/ Do D đối xứng A qua B nên B là trung điểm AD
\(\Rightarrow\left\{{}\begin{matrix}x_D=2x_B-x_A=-1\\y_D=2y_B-y_A=5\end{matrix}\right.\) \(\Rightarrow D\left(-1;5\right)\)
b/ \(\left\{{}\begin{matrix}x_M=\frac{x_A+3x_B}{4}=\frac{3}{2}\\y_M=\frac{y_A+3y_B}{4}=-\frac{5}{4}\end{matrix}\right.\) \(\Rightarrow M\left(\frac{3}{2};-\frac{5}{4}\right)\)