Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ Do D đối xứng A qua B nên B là trung điểm AD
\(\Rightarrow\left\{{}\begin{matrix}x_D=2x_B-x_A=-1\\y_D=2y_B-y_A=5\end{matrix}\right.\) \(\Rightarrow D\left(-1;5\right)\)
b/ \(\left\{{}\begin{matrix}x_M=\frac{x_A+3x_B}{4}=\frac{3}{2}\\y_M=\frac{y_A+3y_B}{4}=-\frac{5}{4}\end{matrix}\right.\) \(\Rightarrow M\left(\frac{3}{2};-\frac{5}{4}\right)\)

a: A(2;4); B(1;0); C(2;2)
vecto AB=(-1;-4)
vecto DC=(2-x;2-y)
Vì ABCD là hình bình hành nên vecto AB=vecto DC
=>2-x=-1 và 2-y=-4
=>x=3 và y=6
c: N đối xứng B qua C
=>x+1=4 và y+0=4
=>x=3 và y=4

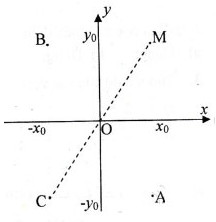
a) Hai điểm đối xứng nhau qua trục hoành thì có hoành độ bằng nhau và tung độ đối nhau.
M0 (x0; y0)=> A(x0;-y0)
b) Hai điểm đối xứng với nhau qua trục tung thì có tung độ bằng nhau còn hoành độ thì đối nhau.
M0 (x0; y0) => B(-x0;y0)
c) Hai điểm đối xứng nhau qua gốc O thì các tọa độ tương ứng đối nhau.
M0 (x0; y0) => C(-x0;-y0)

a) A(3;-5) ; B(1;0)
=> \(\overrightarrow{AB}\left(-2;5\right)\)
Gọi C(x;y) tọa độ cần tìm
khi đó \(\overrightarrow{OC}\left(x;y\right)\)
\(\overrightarrow{OC}=-3\overrightarrow{AB}\Leftrightarrow\left\{{}\begin{matrix}x=-3.\left(-2\right)=6\\y=-3.5=-15\end{matrix}\right.\)
Vậy C(6;-15)
b) D đối xứng với A qua C
=> C trung điểm AD
Gọi D(x1;y1)
Ta có : \(6=\dfrac{3+x_1}{2}\Leftrightarrow x_1=9\)
\(-15=\dfrac{-5+y_1}{2}\) <=> y1 = -25
Vậy D(9;-25)

a) Hai điểm đối xứng nhau qua trục hoành thì có hoành độ bằng nhau và tung độ đối nhau.
M0 (x0; y0)=> A(x0;-y0)
b) Hai điểm đối xứng với nhau qua trục tung thì có tung độ bằng nhau còn hoành độ thì đối nhau.
M0 (x0; y0) => B(-x0;y0)
c) Hai điểm đối xứng nhau qua gốc O thì các tọa độ tương ứng đối nhau.
M0 (x0; y0) => C(-x0;-y0)

a: \(\overrightarrow{AB}=\left(1;5\right)\)
b: Tọa độ trọng tâm G là:
\(\left\{{}\begin{matrix}x=\dfrac{1+2-1}{3}=\dfrac{2}{3}\\y=\dfrac{-2+3-2}{3}=-\dfrac{1}{3}\end{matrix}\right.\)
c: ABCE là hình bình hành
nên vecto AB=vecto EC
=>\(\left\{{}\begin{matrix}-1-x_E=2-1=1\\-2-y_E=3+2=5\end{matrix}\right.\Leftrightarrow E\left(-2;-7\right)\)

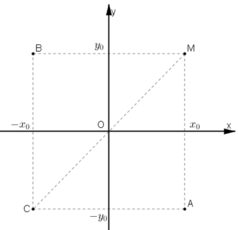
Biểu diễn các điểm trên hệ trục tọa độ ta thấy:
a) Điểm đối xứng với M(x0; y0) qua trục Ox là A(x0 ; –y0)
b) Điểm đối xứng với M(x0 ; y0) qua trục Oy là B(–x0 ; y0)
c) Điểm đối xứng với M(x0 ; y0) qua gốc O là C(–x0 ; –y0).
