Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

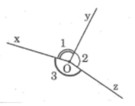
O 1 có đỉnh là O, hai cạnh là Ox và Oy
O 2 có đỉnh là O, hai cạnh là Oy và Oz

a, Tạo thành 4 góc.
b,ta có : xOy+yOx'=180\(^o\)(2 góc kề bù)
mà:xOy-yOx'=30\(^o\)(đbc)
\(\Rightarrow\)xOy=(180\(^o\)+30\(^o\)):2=210\(^o\):2=105\(^o\)
yOx'=105\(^o\)-30\(^o\)=75\(^o\)
Vậy.....

Nhận thấy tứ giác MFNE có góc M và N vuông --> góc MFN+góc MEN= 2 vuông (*)
Lại có các tam giác AFB và MEN đồng dạng (vì có góc NME=gocFAB và góc MNE =góc FBA), suy ra góc AFB=góc MEN --> góc MFN=góc MEN (**), từ (*); (**) suy ra góc MFN=góc MEN =1 vuông
--> tứ giác MENF là hình chữ nhật, từ đó dễ dàng suy ra tiếp FE vuông góc với AB
b) Gọi I ; K lần lượt là trung điểm của O1O2 và MN. Áp dụng Talét dễ dàng tính được IK=5
--> KD^2=ID^2-IK^2 =9^2 -5^2 =56 --> CD=2.KD= 4√14
khó nhỉ ?
Ảnh minh họa O x x' y y' 1 2 3 4
a) \(\widehat{O}_1=65^o\)
Có : \(\widehat{O_1}+\widehat{O_2}=180\) (kề bù)
\(=>\widehat{O_2}=180^o-65^o=115^o\)
Mà theo hình vẽ : \(\widehat{O_2}\) đối đỉnh \(\widehat{O}_4\)
Suy ra: \(\widehat{O_4}=\widehat{O_2}=115^o\)(kề bù)
Rồi có : \(\widehat{O_4}+\widehat{O_3}=180^o=>\widehat{O_3}=65^o\)
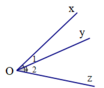
b) \(O_1=2O_2\)
Và : \(O_1+O_2=180^{^O}=>O_1=180^{^O}-O_2\)
\(=>2O_2=180^{^O}-O_2\)
\(=>3O_2=180^{^O}=>O_2=60^{^O}\)
\(O_1=2O_2=>O_1=2.60^{^O}=120^{^O}\)
c) \(\widehat{O_1}-\widehat{O_2}=20^o\)
\(\Leftrightarrow\widehat{O_1}=20+\widehat{O_2}\)
Và : \(\widehat{O_1}+\widehat{O_2}=180^{^O}\)
Ta có hệ sau : \(\left\{{}\begin{matrix}\widehat{O_1}=20^{^o}+\widehat{O_2}\\\widehat{O_1}+\widehat{O_2}=180^{^O}\end{matrix}\right.\)
\(=>20^{^O}+\widehat{O_2}+\widehat{O_2}=180^{^O}\)
\(=>2\widehat{O_2}=160^{^O}=>\widehat{O_2}=80^{^O}\)
\(\widehat{O_1}-80^{^O}=20^{^O}=>\widehat{O_1}=100^{^O}\)
d) \(O_3+O_1=136^{^O}\)
Mà : \(O_3=O_1\) (đối đỉnh)
\(=>O_3=O_1=\dfrac{136^{^O}}{2}=68^{^O}\)