Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Ta có:
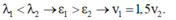
- Áp dụng công thức Einstein về hiệu ứng quang điện cho hai trường hợp ta có:
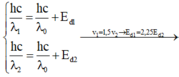
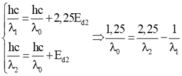
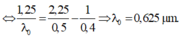

Hệ thức Anh -xtanh trong hiện tượng quang điện ngoài
\(\frac{hc}{\lambda} = A+W_{đmax}\)
mà \(\lambda = \lambda_0/2\) => \(\frac{2hc}{\lambda_0} = A+W_{đmax}\)
Lại có \(A = \frac{hc}{\lambda_0}\) => \(W_{đmax}= \frac{2hc}{\lambda_0} -A= 2A - A = A.\)

Hệ thức Anh -xtanh: \(hf = A+ W_{đ max}= A+eU_h\)
Chiếu bức xạ 1:
\(A = hf_1 - \frac{1}{2}m_e.v_{0max}^2= \frac{6,625.10^{-34}.3.10^8}{0,2.10^{-6}}-\frac{1}{2}9,1.10^{-31}.(0,7.10^6)^2= 7,708.10^{-19}J\)
Chiếu bức xạ 2: \(V_{max}= U_h\)
\(hf_2 = A+eU_h= 7,708.10^{-19}+3.1,6.10^{-19}= 1,25.10^{-18}J\)
=> \(\lambda_2 = \frac{hc}{1,25.10^{-18}}= \frac{6,625.10^{-34}.3.10^8}{1,25.10^{-18}}=1,6.10^{-7}m = 0,16 \mu m.\)

Chiếu bức xạ λ vào quả cầu kim loại cô lập về điện, thì điện thế cực đại là V, ta có: \(\dfrac{hc}{\lambda}=A_t+W_đ\), với \(W_đ=e.V\)
Chiếu bức xạ λ1: \(\dfrac{hc}{\lambda_1}=A_t+W_{đ1}=2W_{đ1}+W_{đ1}=3W_{đ1}=3.eV_1\)
\(\Rightarrow \dfrac{\lambda_1}{hc}=\dfrac{1}{3eV_1}\) (1)
Với \(A_t=2W_{đ1}=2.eV_1\)
Chiếu bức xạ λ2: \(\dfrac{hc}{\lambda_2}=A_t+W_{đ2}=2.eV_1+5eV_1=7eV_1\)
\(\Rightarrow \dfrac{\lambda_2}{hc}=\dfrac{1}{7eV_1}\) \(\Rightarrow \dfrac{\lambda_1-\lambda}{hc}=\dfrac{1}{7eV_1}\) (2)
Lấy (1) - (2) vế với vế: \(\Rightarrow \dfrac{\lambda}{hc}=\dfrac{4}{21.eV_1}\)
\(\Rightarrow \dfrac{hc}{\lambda}=5,25.eV_1=2eV_1+3,25eV_1=A_t+3,25eV_1\)
Suy ra điện thế cực đại của quả cầu là: \(3,25eV_1\)
Chọn C.

Áp dụng: \(\varepsilon=A_t+W_đ\)
Năng lượng \(\varepsilon\) tỉ lệ nghịch với bước sóng
Động năng Wđ tỉ lệ thuận với bình phương vận tốc v
Suy ra:
\(\varepsilon =A_t+W_đ\)(1)
\(\dfrac{\varepsilon}{2} =A_t+\dfrac{W_đ}{k^2}\)(2)
\(\dfrac{\varepsilon}{4} =A_t+\dfrac{W_đ}{10^2}\)(3)
Lấy (1) trừ (2) vế với vế: \(\dfrac{\varepsilon}{2} =(1-\dfrac{1}{k^2})W_đ\)(4)
(1) trừ (3):\(\dfrac{3\varepsilon}{4} =\dfrac{99}{100}W_đ\)(5)
Lấy (4) chia (5) vế với vế: \(\dfrac{2}{3}=(1-\dfrac{1}{k^2}).\dfrac{99}{100}\)
\(\Rightarrow k=\sqrt{\dfrac{200}{97}}\)


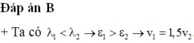
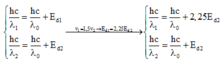
Đáp án D
Ta có:
Từ đó: