Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khi chiếu đồng thời hai bức xạ vào kim loại thì động năng ban đầu cực đại của electron quang điện thoát ra khỏi bề mặt kim loại sẽ có giá trị lớn khi mà bức xạ có bước sóng nhỏ hơn => chọn λ = 0,243 μm.
\(W_{0đ max}= hf - A = hc.(\frac{1}{\lambda}-\frac{1}{\lambda_0})= 6,625.10^{-19}.3.10^8.(\frac{1}{0,243.10^{-6}}-\frac{1}{0,5.10^{-6}})= 4,2.10^{-19}J.\)
=> \(v_{0max}=\sqrt{ \frac{2.W_{0đ max}}{m_e}}= 9,61.10^5 m/s.\)

Hệ thức Anh -xtanh: \(hf = A+ W_{đ max}= A+eU_h\)
Chiếu bức xạ 1:
\(A = hf_1 - \frac{1}{2}m_e.v_{0max}^2= \frac{6,625.10^{-34}.3.10^8}{0,2.10^{-6}}-\frac{1}{2}9,1.10^{-31}.(0,7.10^6)^2= 7,708.10^{-19}J\)
Chiếu bức xạ 2: \(V_{max}= U_h\)
\(hf_2 = A+eU_h= 7,708.10^{-19}+3.1,6.10^{-19}= 1,25.10^{-18}J\)
=> \(\lambda_2 = \frac{hc}{1,25.10^{-18}}= \frac{6,625.10^{-34}.3.10^8}{1,25.10^{-18}}=1,6.10^{-7}m = 0,16 \mu m.\)

Đáp án: C
Vận tốc ban đầu cực đại của các electron quang điện băng
h c λ = h c λ 0 + m v 1 2 2 ⇒ v 1 = 2 m . h c λ - h c λ 0 = 2 9 , 1 . 10 - 31 6 , 625 . 10 - 34 . 3 . 10 8 0 , 243 . 10 - 6 - 6 , 625 . 10 - 34 . 3 . 10 8 0 , 5 . 10 - 6

a. Bước sóng của chùm sáng: \(\lambda=\dfrac{c}{f}=\dfrac{3.10^8}{10^{15}}=0,3\mu m\)
Giới hạn quang điện: \(\lambda_0=\dfrac{hc}{A_t}=\dfrac{6,625.10^{-34}.3.10^8}{5,15.1,6.10^{-19}}=0,24.19^-6m=0,24\mu m\)
Do \(\lambda > \lambda_0\) nên không xảy ra hiện tượng quang điện.
b. Ta có: \({W_{d0}} = \frac{{hc}}{\lambda } - A = 1,{7.10^{ - 19}}J\Rightarrow {v_0} = \sqrt {\frac{{2{W_{d0}}}}{m}} = 0,{6.10^6}m/s\)
c. \({n_e} = \frac{{{I_{bh}}}}{e} = 2,{8.10^{13}};\,\,\,\,\,\,{n_\lambda } = \frac{P}{{\frac{{hc}}{\lambda }}} = \frac{{P\lambda }}{{hc}} ={3.10^{15}} \Rightarrow H = \frac{{{n_e}}}{{{n_\lambda }}} = 9,{3.10^{ - 3}} = 0,93\% \)
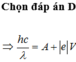
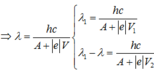
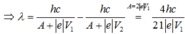
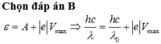
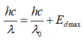
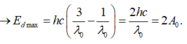
Mình hướng dẫn thế này rồi bạn làm tiếp nhé.
a. Áp dụng CT: \(hf=A_t+\dfrac{1}{2}mv^2\)
\(\Rightarrow 6,625.10^{-34}.3.10^8=A_t+\dfrac{1}{2}.9,1.10^{-31}.(0,4.10^6)^2\)
\(\Rightarrow A_t\)
Mà \(A_t=\dfrac{hc}{\lambda_0}\Rightarrow \lambda_0\)
b. Áp dụng: \(\dfrac{hc}{\lambda}=A_t+eV_{max}\)
\(\Rightarrow \lambda\)