Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi O là tâm đường tròn \(\Rightarrow\) O là trung điểm BC
\(\stackrel\frown{BE}=\stackrel\frown{ED}=\stackrel\frown{DC}\Rightarrow\widehat{BOE}=\widehat{EOD}=\widehat{DOC}=\dfrac{180^0}{3}=60^0\)
Mà \(OD=OE=R\Rightarrow\Delta ODE\) đều
\(\Rightarrow ED=R\)
\(BN=NM=MC=\dfrac{2R}{3}\Rightarrow\dfrac{NM}{ED}=\dfrac{2}{3}\)
\(\stackrel\frown{BE}=\stackrel\frown{DC}\Rightarrow ED||BC\)
Áp dụng định lý talet:
\(\dfrac{AN}{AE}=\dfrac{MN}{ED}=\dfrac{2}{3}\Rightarrow\dfrac{EN}{AN}=\dfrac{1}{2}\)
\(\dfrac{ON}{BN}=\dfrac{OB-BN}{BN}=\dfrac{R-\dfrac{2R}{3}}{\dfrac{2R}{3}}=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{EN}{AN}=\dfrac{ON}{BN}=\dfrac{1}{2}\) và \(\widehat{ENO}=\widehat{ANB}\) (đối đỉnh)
\(\Rightarrow\Delta ENO\sim ANB\left(c.g.c\right)\)
\(\Rightarrow\widehat{NBA}=\widehat{NOE}=60^0\)
Hoàn toàn tương tự, ta có \(\Delta MDO\sim\Delta MAC\Rightarrow\widehat{MCA}=\widehat{MOD}=60^0\)
\(\Rightarrow\Delta ABC\) đều

\(\sqrt{1-x-2x^2}=\sqrt{\left(1+x\right)\left(1-2x\right)}\le\dfrac{1+x-2x+1}{2}=\dfrac{-x+2}{2}\)
(AM-GM)
do đó \(A\le\dfrac{x}{2}+\dfrac{-x+2}{2}=1\)
Dấu = xảy ra khi 1+x=1-2x <=> x=0 (tmđk)

\(\sqrt{2x-1}=t\Leftrightarrow2x-1=t^2\)\(\Leftrightarrow x=\dfrac{t^2+1}{2}\).

a: \(=\left|x-4\right|-\left|x-2\right|\)
\(=\left|3\sqrt{2}-1-4\right|-\left|3\sqrt{2}-1-2\right|\)
\(=5-3\sqrt{2}-\left(3\sqrt{2}-3\right)=-6\sqrt{2}+8\)
b: \(=\left|\sqrt{x-1}+1\right|+\left|\sqrt{x-1}-1\right|\)
\(=\left|\sqrt{7}-1+1\right|+\left|\sqrt{7}-1-1\right|\)
\(=\sqrt{7}+4-\sqrt{7}=4\)

1, đk: \(x>0\) và \(x\ne4\)
Ta có: A=\(\dfrac{1}{2\sqrt{x}-x}=\dfrac{1}{-\left(x-2\sqrt{x}+1\right)+1}=\dfrac{1}{-\left(\sqrt{x}-1\right)^2+1}\)
Ta luôn có: \(-\left(\sqrt{x}-1\right)^2\le0\) với \(x>0\) và \(x\ne4\)
\(\Rightarrow-\left(\sqrt{x}-1\right)^2+1\le1\)
\(\Rightarrow A\ge1\). Dấu "=" xảy ra <=> x=1 (t/m)
Vậy MinA=1 khi x=1
2, đk: \(x\ge0;x\ne1;x\ne9\)
Ta có: B=\(\dfrac{1}{x-4\sqrt{x}+3}=\dfrac{1}{\left(x-4\sqrt{x}+4\right)-1}=\dfrac{1}{\left(\sqrt{x}-2\right)^2-1}\)
Ta luôn có: \(\left(\sqrt{x}-2\right)^2\ge0\) với \(x\ge0;x\ne1;x\ne9\)
\(\Rightarrow\left(\sqrt{x}-2\right)^2-1\ge-1\)
\(\Rightarrow B\le-1\). Dấu "=" xảy ra <=> x=4 (t/m)
Vậy MaxB=-1 khi x=4
3, đk: \(x\ge0;x\ne15+4\sqrt{11}\)
Ta có: C=\(\dfrac{1}{4\sqrt{x}-x+7}=\dfrac{1}{-\left(x-4\sqrt{x}+4\right)+11}=\dfrac{1}{-\left(\sqrt{x}-2\right)^2+11}\)
Ta luôn có: \(-\left(\sqrt{x}-2\right)^2\le0\) với \(x\ge0;x\ne15+4\sqrt{11}\)
\(\Rightarrow-\left(\sqrt{x}-2\right)^2+11\le11\)
\(\Rightarrow C\ge\dfrac{1}{11}\). Dấu "=" xảy ra <=> x=4 (t/m)
Vậy MinC=\(\dfrac{1}{11}\) khi x=4

Bởi vì \(\sqrt{2x+1}\ge0\)mà \(x>\sqrt{2x+1}\)nên phải có điều kiện \(x>0\)

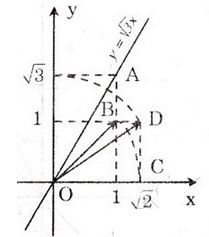
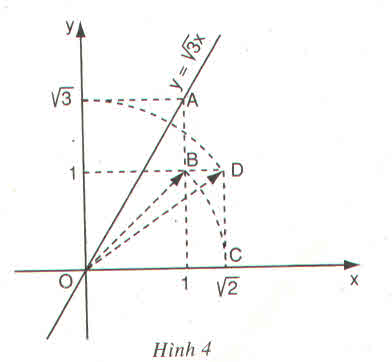
Ta có: \(\sqrt{3}\) = \(\sqrt{2+1}\) = \(\sqrt{\left(\sqrt{2}\right)^2+1^2}\)
Hình vẽ SGK có : OC = OB = \(\sqrt{2}\) và theo định lí Py-ta-go t a có :
OD = \(\sqrt{OC^2+CD^2}\)= \(\sqrt{\left(\sqrt{2}\right)^2+1^2}\)= \(\sqrt{3}\)
Dùng compa ta xác định được điểm biểu diễn số \(\sqrt{3}\). trên Oy. Từ đó xác định được điểm A.

1. \(\left(1+\dfrac{a+\sqrt{a}}{\sqrt{a}+1}\right)\left(1-\dfrac{a-\sqrt{a}}{\sqrt{a}-1}\right)\)
\(=\left(1+\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)}{\sqrt{a}+1}\right)\left(1-\dfrac{\sqrt{a}\left(\sqrt{a}-1\right)}{\sqrt{a}-1}\right)\)
\(=\left(1+\sqrt{a}\right)\left(1-\sqrt{a}\right)=1-a\)
2. a) Với a>b>0 thì
\(Q=\dfrac{a}{\sqrt{a^2-b^2}}-\left(1+\dfrac{a}{\sqrt{a^2-b^2}}\right):\dfrac{b}{a-\sqrt{a^2-b^2}}\)
\(=\dfrac{a}{\sqrt{a^2-b^2}}-\dfrac{a+\sqrt{a^2-b^2}}{\sqrt{a^2-b^2}}.\dfrac{a-\sqrt{a^2-b^2}}{b}\)
\(=\dfrac{a}{\sqrt{a^2-b^2}}-\dfrac{a^2-\left(a^2-b^2\right)}{b\sqrt{a^2-b^2}}\)
\(=\dfrac{a}{\sqrt{a^2-b^2}}-\dfrac{b^2}{b\sqrt{a^2-b^2}}=\dfrac{a}{\sqrt{a^2-b^2}}-\dfrac{b}{\sqrt{a^2-b^2}}\)
\(=\dfrac{a-b}{\sqrt{a^2-b^2}}=\dfrac{a-b}{\sqrt{a-b}.\sqrt{a+b}}=\sqrt{\dfrac{a-b}{a+b}}\)
b) Thay a = 3b ta được
\(Q=\sqrt{\dfrac{a-b}{a+b}}=\sqrt{\dfrac{3b-b}{3b+b}}=\sqrt{\dfrac{2b}{4b}}=\sqrt{\dfrac{1}{2}}=\dfrac{\sqrt{2}}{2}\)
1) d) ta có : \(VT=\left(1+\dfrac{a+\sqrt{a}}{\sqrt{a}+1}\right)\left(1-\dfrac{a-\sqrt{a}}{\sqrt{a}-1}\right)\)
\(\Leftrightarrow\left(1+\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)}{\sqrt{a}+1}\right)\left(1-\dfrac{\sqrt{a}\left(\sqrt{a}-1\right)}{\sqrt{a}-1}\right)\)
\(\Leftrightarrow\left(1+\sqrt{a}\right)\left(1-\sqrt{a}\right)=1-a=VP\)
\(\Rightarrow\) \(\left(1+\dfrac{a+\sqrt{a}}{\sqrt{a}+1}\right)\left(1-\dfrac{a-\sqrt{a}}{\sqrt{a}-1}\right)=1-a\) (đpcm)
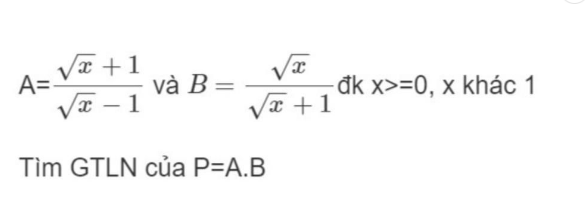







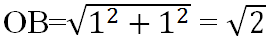
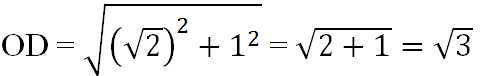
Đơn giản là em đang xem một lời giải sai. Việc khẳng định $P\leq 0$ hoặc $P>0$ rồi kết luận hàm số không có GTLN là sai.
Bởi vậy những câu hỏi ở dưới là vô nghĩa.
Việc gọi $P$ là hàm số lên lớp cao hơn em sẽ được học, còn bây giờ chỉ cần gọi đơn giản là phân thức/ biểu thức.
Hàm số, có dạng $y=f(x)$ biểu diễn mối liên hệ giữa biến $x$ với biến phụ thuộc $y$. Mỗi giá trị của $x$ ta luôn xác định được một giá trị tương ứng của $y$.
$P=AB=\frac{\sqrt{x}}{\sqrt{x}-1}=1+\frac{1}{\sqrt{x}-1}$
Để $P_{\max}$ thì $\frac{1}{\sqrt{x}-1}$ max
Điều này xảy ra khi $\sqrt{x}-1$ min và có giá trị dương
$\Leftrightarrow x>1$ và $x$ nhỏ nhất
Trong tập số thực thì em không thể tìm được số lớn hơn 1 mà nhỏ nhất được. Như kiểu $1,00000000000000000000....$ (vô hạn đến không biết khi nào thì kết thúc)
Do đó $P$ không có max
Min cũng tương tự, $P$ không có min.