Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Dãy số chỉ khối lượng còn lại của 20 gam poloni 210 sau \(n\) chu kì là một cấp số nhân có số hạng đầu \({u_1} = 20\) và công bội \(q = \frac{1}{2}\).
a) Sau 690 ngày thì số chu kì bán rã thực hiện được là: \(690:138 = 5\) (chu kì).
Vậy khối lượng còn lại của 20 gam poloni 210 là: \({u_5} = {u_1}.{q^4} = 20.{\left( {\frac{1}{2}} \right)^4} = 1,25\) (gam).
b) Sau 7314 ngày thì số chu kì bán rã thực hiện được là: \(7314:138 = 53\) (chu kì).
Vậy khối lượng còn lại của 20 gam poloni 210 là: \({u_{53}} = {u_1}.{q^{52}} = 20.{\left( {\frac{1}{2}} \right)^{52}} \approx 44,{4.10^{ - 16}}\) (gam).

a) Với \({M_0} = 200,T = 9,M\left( t \right) = 100\) ta có:
\(100 = 200{\left( {\frac{1}{2}} \right)^{\frac{t}{9}}} \Leftrightarrow {\left( {\frac{1}{2}} \right)^{\frac{t}{9}}} = \frac{1}{2} \Leftrightarrow \frac{t}{9} = 1 \Leftrightarrow t = 9\)
Vậy sau 9 giờ thì khối lượng plutonium-234 ban đầu 200 g còn lại là 100 g.
b) Với \({M_0} = 200,T = 9,M\left( t \right) = 50\) ta có:
\(50 = 200{\left( {\frac{1}{2}} \right)^{\frac{t}{9}}} \Leftrightarrow {\left( {\frac{1}{2}} \right)^{\frac{t}{9}}} = \frac{1}{4} \Leftrightarrow {\left( {\frac{1}{2}} \right)^{\frac{t}{9}}} = {\left( {\frac{1}{2}} \right)^2} \Leftrightarrow \frac{t}{9} = 2 \Leftrightarrow t = 18\)
Vậy sau 18 giờ thì khối lượng plutonium-234 ban đầu 200 g còn lại là 50 g.
c) Với \({M_0} = 200,T = 9,M\left( t \right) = 20\) ta có:
\(20 = 200{\left( {\frac{1}{2}} \right)^{\frac{t}{9}}} \Leftrightarrow {\left( {\frac{1}{2}} \right)^{\frac{t}{9}}} = \frac{1}{{10}} \Leftrightarrow \frac{t}{9} = {\log _{\frac{1}{2}}}\frac{1}{{10}} \Leftrightarrow \frac{t}{9} = {\log _2}10 \Leftrightarrow t = 9{\log _2}10 \approx 29,9\)
Vậy sau 29,9 giờ thì khối lượng plutonium-234 ban đầu 200 g còn lại là 50 g.

a) Nhận xét: u1 = ; u2 =
; u3 =
; ... un =
.
Điều này chứng minh đơn giản bằng quy nạp.
b) lim un = lim ()n= 0 = vì lim qn = 0 nếu |q| < 1.
c) Đổi 10-6 g = .
kg =
kg.
Muốn có un = <
, ta cần chọn n0 sao cho 2n0 > 109. Chẳng hạn, với n0 = 36, thì
236 = (24)9 = 16 9 > 109. Nói cách khác, sau chu kì thứ 36 (nghĩa là sau 36.24000 = 864 000 (năm), chúng ta không còn lo lắng về sự độc hại của khối lượng chất phóng xạ còn lại.

a. Sau 1 chu kì bán rã: 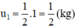
Sau 2 chu kì bán rã: 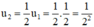
Sau 3 chu kì bán rã: 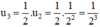
…
Tổng quát : Sau n chu kì bán rã : 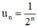
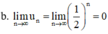
c. Chất phóng xạ không còn độc hại nữa khi khối lượng chất phóng xạ còn lại < 10-6 g = 10-9 kg
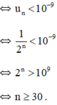
Vậy sau 30 chu kì = 30.24000 = 720 000 năm thì 1kg chất phóng xạ này không còn độc hại nữa.

a: Khối lượng của vật thời điểm t=0 là: \(m\left(0\right)=13\cdot e^{-0.015\cdot0}=13\left(kg\right)\)
b: Sau 45 ngày khối lượng còn lại là;
\(m\left(45\right)=13\cdot e^{-0.015\cdot45}\simeq6,62\left(kg\right)\)

a: Nhiệt độ ban đầu là:
\(T=25+70\cdot e^{-0.5\cdot0}=95\left(^0C\right)\)
b: ĐặtT=30
=>\(25+70\cdot e^{-0.5t}=30\)
=>\(e^{-0.5t}=\dfrac{1}{14}\)
=>\(-0.5t=ln\left(\dfrac{1}{14}\right)\)
=>\(t\simeq5,28\simeq6\)
=>Sau 6 phút thì nhiệt độ còn lại tầm 30 độ C

tham khảo
a) Khối lượng vi khuẩn tại thời điểm bắt đầu nuôi cấy là:
\(M\left(0\right)=50.1,06^0=50\left(g\right)\)
b) Khối lượng vi khuẩn sau \(2\) giờ là:
\(M\left(2\right)=50.1,06^2=56,18\left(g\right)\)
Khối lượng vi khuẩn sau \(10\) giờ là:
\(M\left(10\right)=50.1,06^{10}\approx89,54\left(g\right)\)
c) Xét hàm số \(M\left(t\right)=50.1,06^t\).
Vì \(1,06>1\) nên hàm số \(M\left(t\right)=50.1,06^t\) là hàm số đồng biến. Vậy khối lượng vi khuẩn tăng dần theo thời gian.

a) Sau một chu kì bán rã \({u_1} = 1.\frac{1}{2} = \frac{1}{2}\left( {kg} \right)\)
Sau hai chu kì bán rã \({u_2} = \frac{1}{2}.{u_1} = \frac{1}{{{2^2}}}\left( {kg} \right)\)
…
Vậy sau n chu kì bán rã \({u_n} = \frac{1}{{{2^n}}}\)
b) \(\lim {u_n} = \lim \frac{1}{{{2^n}}} = \lim {\left( {\frac{1}{2}} \right)^n} = 0\)
c) Đổi \({10^{ - 6}}g = {10^{ - 9}}kg\)
Vì chất phóng xạ này sẽ không độc hại nữa nếu khối lượng chất phóng xạ còn lại bé hơn \({10^{ - 6}}\) g nên ta có
\({u_n} < {10^{ - 9}} \Leftrightarrow \frac{1}{{{2^n}}} < {10^{ - 9}} \Leftrightarrow {2^n} > {10^9} \Leftrightarrow n > {\log _2}{10^9} \approx 29,9\)
Vậy sau 30 chu kì là 30.24 000 = 720 000 năm thì khối lượng chất phóng xạ đã cho ban đầu không còn độc hại đối với con người.
a, Khối lượng polonium-210 còn lại sau 2 năm là:
\(M\left(730\right)=100\cdot\left(\dfrac{1}{2}\right)^{\dfrac{730}{138}}\approx1,92\left(g\right)\)
b, Ta có:
\(M\left(t\right)=40\\ \Leftrightarrow40=100\cdot\left(\dfrac{1}{2}\right)^{\dfrac{t}{138}}\\ \Leftrightarrow\left(\dfrac{1}{2}\right)^{\dfrac{t}{138}}=\dfrac{4}{10}\\ \Leftrightarrow\dfrac{t}{138}=log_{\dfrac{1}{2}}\left(\dfrac{4}{10}\right)\\ \Leftrightarrow t=138\cdot log_{\dfrac{1}{2}}\left(\dfrac{4}{10}\right)\approx182,43\)
Vậy sau 183,43 ngày thì còn lại 40g polonium-210.