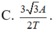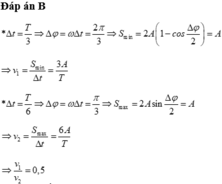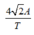Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn A
Ta dựa vào tính chất của dao động là vật chuyển động càng nhanh khi càng gần vị trí cân bằng cho nên quãng đường dài nhất DS vật đi được trong thời gian Dt với 0 < Dt < T/2 phải đối xứng qua vị trí cân bằng (hình vẽ)
Với thời gian t = 2T/3 = T/2 + T/6 → S = 2A + ∆S (∆φ = 60o)
Do vậy, tốc độ trung bình lớn nhất của vật thực hiện được trong khoảng thời gian 2T/3 khi vật đi được quảng đường lớn nhất trong khoảng thời gian 2T/3 →∆S phải lớn nhất
→ 
= 2A.sin(60/2) = A →Smax = 3A
→ tốc độ trung bình lớn nhất = Smax / t = 9A/2
Đáp án A
Tốc độ trung bình của vật trong khoảng thời gian
bằng 
Với S là quãng đường vật đi trong thời gian Δt.
⇒Tốc độ trung bình lớn nhất của vật trong khoảng thời gian đó bằng
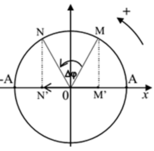
Trong cùng thời gian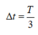 
vật đi được quãng đường dài nhất khi đi quanh vị trí cân bằng, đi từ điểm P1 đến điểm P2 (P1 và P2 là hai điểm đối xứng nhau qua vị trí cân bằng O của vật). Sử dụng mối quan hệ giữa dao động điều hòa và chuyển động tròn đều.
→ thời gian ngắn nhất vật đi từ P1 đến O bằng thời gian ngắn nhất vật đi từ O đến P2 và bằng 
và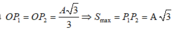 
→ Tốc độ trung bình lớn nhất của vật trong khoảng thời gian đó bằng
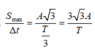
Đáp án D
Vì trong một chu kỳ dao động lò xo bị giãn bằng 3 lần thời gian lò xo bi nén nên góc quay mà vecto quay được khi lò xo giãn cũng bằng 3 lần góc quay khi lò xo bị nén. Ta có hệ:
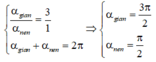
nên ta sẽ được
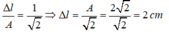
Chu kỳ của vật là:
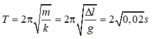
Tốc độ trung bình của vật trong khoảng thời gian lò xo bị nén trong một chu kỳ bằng: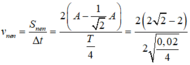 
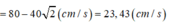
Tốc độ trung bình = quãng đường đi được trong thời gian t chia cho thời gian đi.
\(v=\frac{s}{t}.\)
v min khi s min.
s min khi quãng đường đi được ứng với một cung tròn \(\widehat{aNb}\) lấy biên làm trung điểm. Như hình tròn ở dưới. (Nếu S max thì quãng đường đi được ứng với cung tròn lấy vị trí cân bằng làm trung điểm)
MNabphi
\(t=\frac{T}{6}\Rightarrow\widehat{aNb}=t.\omega=\frac{2T}{3}.\frac{2\pi}{T}=\frac{4\pi}{3}>\pi.\)
\(S_{min}=s_1\left(\pi\right)+s_{2min}\left(\frac{\pi}{3}\right)\)Do cung lớn hơn 180 độ ta tách \(\pi+\frac{\pi}{3}.\)
\(s_1\left(\pi\right)=2A.\) là quãng đường đi được ứng với cung 180 độ.
Tính quãng đường nhỏ nhất đi được ứng với cung 60 độ \(s_{2min}\left(\frac{\pi}{3}\right)\)
=> \(\varphi=\frac{\frac{\pi}{3}}{2}=\frac{\pi}{6}.\)
Tương ứng với cung tròn \(aNb\) là \(s_{2min}=2.MN=2.\left(A-A\cos\varphi\right)=2A\left(1-\cos\varphi\right).\)
\(s_{min}=s_1+s_2=2A+2A\left(1-\cos30\right)=9,07cm.\)
vận tốc trung bình là \(v=\frac{s}{t}=\frac{9,07}{\frac{2T}{3}}=13,6\)cm/s.